Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 3164 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 11650 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 27-Απρ-2024 | Ύλη: | ||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 11650 | ||
| Ύλη: | |||
| Τελευταία Ενημέρωση: 27-Απρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ Δ
Μεταλλικός κύβος έλκεται με τη βοήθεια ενός ηλεκτροκινητήρα, πάνω σε οριζόντιο διάδρομο. Στον κύβο ασκείται σταθερή οριζόντια δύναμη \(\vec{F}\) και κινείται ευθύγραμμα με σταθερή επιτάχυνση. Με τη βοήθεια συστήματος φωτοπυλών παίρνουμε την πληροφορία ότι το μέτρο της ταχύτητας του κύβου τη χρονική στιγμή \(t_0 = 0\) είναι ίσο με \(2\ \dfrac{m}{s}\) και τη χρονική στιγμή \(t_1 = 2\ s\) είναι ίσο με \(12\ \dfrac{m}{s}\).
Η μέση ισχύς του ηλεκτροκινητήρα (ο μέσος ρυθμός προσφερόμενης ενέργειας στον κύβο μέσω του έργου της δύναμης \(\vec{F}\)), στο παραπάνω χρονικό διάστημα των \(2\ s\) είναι \(Ρ_μ = 98\ W\). Επίσης, έχει μετρηθεί πειραματικά ο συντελεστής τριβής ολίσθησης μεταξύ του κύβου και του διαδρόμου και βρέθηκε ίσος με \(0,2\). Δίνεται η επιτάχυνση της βαρύτητας \(g = 10\ \dfrac{m}{s^2}\) και ότι η επίδραση του αέρα θεωρείται αμελητέα.
Να υπολογίσετε:
Δ1) το μέτρο της επιτάχυνσης με την οποία κινείται ο κύβος,
Μονάδες 5
Δ2) την ενέργεια που μεταφέρθηκε στον κύβο μέσω του έργου της δύναμης \(\vec{F}\) στο χρονικό διάστημα των \(2\ s\),
Μονάδες 6
Δ3) το μέτρο της δύναμης \(\vec{F}\).
Μονάδες 7
Δ4) τη μάζα του κύβου.
Μονάδες 7
Ενδεικτική λύση
Δ1) Από την εξίσωση της επιτάχυνσης στην ευθύγραμμη ομαλά επιταχυνόμενη κίνηση:
$$α=\dfrac{Δυ}{Δt}$$ $$\Rightarrow α=\dfrac{12-2}{2}$$ $$\Rightarrow α = 5\ \dfrac{m}{s}$$
Δ2) Με χρήση του δεδομένου της μέσης ισχύος υπολογίζουμε το έργο της δύναμης \(\vec{F}\):
$$P_{μ}=\dfrac{W_{F}}{Δt}$$ $$\Rightarrow W_{F}=P_{μ}\cdot Δt$$ $$\Rightarrow W_{F}=98\cdot 2$$ $$\Rightarrow W_{F}=196\ J$$
Δ3) Από την εξίσωση της μετατόπισης στην ευθύγραμμη ομαλά επιταχυνόμενη κίνηση υπολογίζουμε την μετατόπιση του κύβου από την \(t_0 = 0\) έως την \(t_1 = 2\ s\):
$$Δx=υ_{0}\cdot t+\dfrac{1}{2}\cdot a\cdot t^{2}$$ $$\Rightarrow Δx=14\ m$$
Και στη συνέχεια το μέτρο της δύναμης \(\vec{F}\):
$$W_{F}=F\cdot Δx\cdot συν0^{0}$$ $$\Rightarrow F=14\ N$$
Δ4)
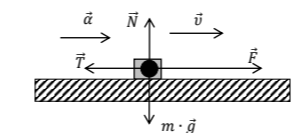
Εφαρμόζουμε τον 1ο νόμο του Newton στον κατακόρυφο άξονα:
$$\sum{\vec{F}}=0$$ $$\Rightarrow Ν=m\cdot g$$
Ισχύει:
$$Τ=μ\cdot Ν$$ $$\Rightarrow Τ=μ\cdot m\cdot g$$
Και τον 2ο νόμο του Newton στον οριζόντιο άξονα λαμβάνοντας ως θετική τη φορά της επιτάχυνσης:
$$F-Τ=m\cdot a$$ $$\Rightarrow F=μ\cdot m\cdot g+m\cdot a$$ $$\Rightarrow m=\dfrac{F}{μ\cdot g+a}$$ $$\Rightarrow m=2\ Kg$$