Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 42577 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 12354 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 21-Μαΐ-2022 | Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 1.1.5. Η έννοια της ταχύτητας στη ευθύγραμμη ομαλή κίνηση 1.1.6. Η έννοια της μέσης ταχύτητας | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 12354 | ||
| Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 1.1.5. Η έννοια της ταχύτητας στη ευθύγραμμη ομαλή κίνηση 1.1.6. Η έννοια της μέσης ταχύτητας | ||
| Τελευταία Ενημέρωση: 21-Μαΐ-2022 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
Θέμα 4ο
Πομπός GPS στερεώνεται στο σώμα ενός παπαγάλου ώστε να στέλνει διαρκώς την θέση του σε ερευνητές που τον παρακολουθούν. Ο παπαγάλος αφήνεται ελεύθερος και η πορεία του καταγράφεται στο πιο κάτω διάγραμμα. Θεωρούμε ότι το εργαστήριο από το οποίο ξεκινάει σε χρόνο
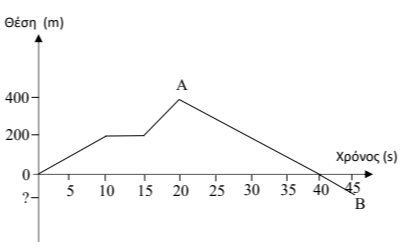
Καλείστε να βοηθήσετε τη μελέτη της κίνησης του πτηνού. Υπολογίστε:
4.1) τη μέση ταχύτητα του παπαγάλου από τη χρονική στιγμή της εκκίνησης μέχρι τη χρονική στιγμή
4.2) τη μέση ταχύτητα του παπαγάλου από τη χρονική στιγμή της εκκίνησης, μέχρι τη χρονική στιγμή
4.3) τη θέση του πτηνού τη χρονική στιγμή
4.4) Σχεδιάστε σε βαθμολογημένους άξονες το διάγραμμα της τιμής της ταχύτητας σε συνάρτηση με το χρόνο.
(Μονάδες 6+7+6+6)
Ενδεικτική Λύση
4.1) Οι πληροφορίες που παίρνουμε από το διάγραμμα για την κίνηση του παπαγάλου σε μορφή πίνακα:
| Χρονικό Διάστημα | Είδος Κίνησης |
|---|---|
| Ευθύγραμμη Ομαλή Κίνηση | |
| Ακινησία | |
| Ευθύγραμμη Ομαλή Κίνηση | |
| Ευθύγραμμη Ομαλή Κίνηση (επιστρέφει προς την αφετηρία) | |
| Ευθύγραμμη Ομαλή Κίνηση (προσπερνά την αφετηρία και συνεχίζει προς την αντίθετη κατεύθυνση |
Με βάση το διάγραμμα ο παπαγάλος διανύει
(Μονάδες 6)
4.2) Στο χρονικό διάστημα από
Άρα, η ταχύτητα του
Άρα για το χρονικό διάστημα
(Μονάδες 3)
Οπότε η συνολική απόσταση για τα πρώτα
Η μέση ταχύτητα για τα πρώτα
(Μονάδες 4)
4.3) Για το κομμάτι της διαδρομής
Για το χρονικό διάστημα
Eπειδή κινείται σε μια ευθεία, θα βρίσκεται σε απόσταση
(Μονάδες 6)
4.4) Για να σχεδιάσουμε το διάγραμμα της ταχύτητας ως προς το χρόνο χρειάζεται να υπολογίσουμε την ταχύτητα για το χρονικό διάστημα
Και για το χρονικό διάστημα
(Μονάδες 6)
Σημείωση: Εάν παρατηρούσαμε ένα διάγραμμα της ταχύτητας ως προς το χρόνο βασισμένο σε πραγματικές τιμές από αντίστοιχες παρατηρήσεις / κινήσεις πτηνών, δε θα βλέπαμε αυτές τις απότομες αλλαγές ταχύτητας και κατεύθυνσης. Θα ήταν διαρκώς μεταβαλλόμενο κατά τη διάρκεια της πτήσης, με επιταχύνσεις και επιβραδύνσεις κατά τη διάρκεια του πετάγματος και πριν/μετά τις στάσεις του. Για τις ανάγκες της άσκησης χρησιμοποιήθηκαν εξιδανικευμένα δεδομένα που επιτρέπουν την αναπαράσταση και επεξεργασία με γνώσεις της Α΄ Λυκείου.
