Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 10618 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 14217 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 15-Απρ-2024 | Ύλη: | 1.1.8 Η έννοια της επιτάχυνσης στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.1.9. Οι εξισώσεις προσδιορισμού της ταχύτητας και της θέσης ενός κινητού στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 1.3.7 Ο νόμος της τριβής 2.1.1 Η έννοια του έργου | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 14217 | ||
| Ύλη: | 1.1.8 Η έννοια της επιτάχυνσης στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.1.9. Οι εξισώσεις προσδιορισμού της ταχύτητας και της θέσης ενός κινητού στην ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 1.2.4 Ο δεύτερος νόμος του Νεύτωνα ή Θεμελιώδης νόμος της Μηχανικής 1.3.7 Ο νόμος της τριβής 2.1.1 Η έννοια του έργου | ||
| Τελευταία Ενημέρωση: 15-Απρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
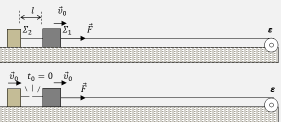
Ένας μηχανισμός \(ε\) (εργάτης), είναι στερεωμένος στο άκρο μιας οριζόντιας ράμπας μεγάλου μήκους και σέρνει ένα σύστημα δύο κιβωτίων, με τη βοήθεια αβαρούς και μη ελαστικού νήματος.
Τα δύο κιβώτια \(Σ_{1}\) και \(Σ_{2}\) έχουν μάζες \(m_{1}=2\ Kg\) και \(m_{2}=1\ Kg\) αντίστοιχα και είναι μεταξύ τους δεμένα με οριζόντιο και τεντωμένο νήμα, αβαρές και μη ελαστικό, μήκους \(l=12,5\ cm\), όπως στην εικόνα. Τα δύο κιβώτια εμφανίζουν τριβή με το επίπεδο της ράμπας, με ίδιο συντελεστή τριβής ολίσθησης \(μ=0,25\).
Το νήμα του μηχανισμού είναι δεμένο στο κιβώτιο \(Σ_{1}\), ασκεί σε αυτό σταθερή οριζόντια δύναμη \(\vec{F}\) και το αποτέλεσμα είναι το σύστημα των δύο κιβωτίων, να κινείται ευθύγραμμα με σταθερή ταχύτητα \(\vec{υ}_{0}\), μέτρου \(υ_{0}=2,5\ \dfrac{m}{s}\).
4.1 Να υπολογίσετε το μέτρο της δύναμης \(\vec{F}\).
Μονάδες 6
Τη χρονική στιγμή \(t_{0}=0\) το νήμα που συνδέει τα δύο κιβώτιακόβεται, ενώ η δύναμη που ασκεί ο μηχανισμός διατηρείται σταθερή.
4.2 Να υπολογίσετε το μέτρο της επιτάχυνσης του σώματος \(Σ_{1}\) και το μέτρο της επιβράδυνσης του σώματος \(Σ_{2}\), μετά το κόψιμο του νήματος.
Μονάδες 6
4.3 Πόσο απέχουν μεταξύ τους τα δύο σώματα, τη στιγμή \(t_{1}\) κατά την οποία ακινητοποιείται το σώμα \(Σ_{2}\) ;
Μονάδες 7
4.4 Πόση ενέργεια μεταφέρθηκε στο σώμα \(Σ_{1}\) από τον μηχανισμό, από τη στιγμή που κόπηκε το νήμα, μέχρι τη στιγμή κατά την οποία έχει διανύσει 3 m;
Μονάδες 6
Δίνεται το μέτρο της επιτάχυνσης βαρύτητας \(g=10\ \dfrac{m}{s^{2}}\) και ότι οι αντιστάσεις αέρα αγνοούνται.
ΘΕΜΑ 4 (Ενδεικτικές απαντήσεις)
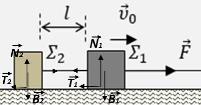
4.1 Στην κατακόρυφη διεύθυνση (διεύθυνση y) οι δυνάμεις ισορροπούν σε κάθε σώμα. Άρα ισχύουν:
$$Σ_{1} : ΣF_{y}=N_{1}-B_{1}=0$$
Άρα, \(N_{1}=B_{1}=m_{1}\cdot g=20N\)
$$Σ_{2} : ΣF_{y}=N_{2}-B_{2}=0$$
Άρα, \(N_{2}=B_{2}=m_{2}\cdot g=10N\)
Εφαρμόζοντας τον νόμο της τριβής, υπολογίζουμε τα μέτρα των τριβών στα δύο σώματα:
$$T_{1}=μ\cdot N_{1}=0,25\cdot 20N=5 N$$
$$T_{2}=μ\cdot N_{2}=0,25\cdot 10N=2,5 N$$
Επειδή στην οριζόντια διεύθυνση τα σώματα κινούνται με σταθερή ταχύτητα, οι δυνάμεις ισορροπούν και στη διεύθυνση αυτή (διεύθυνση x). Εφαρμόζοντας τον πρώτο νόμο του Νεύτωνα για το σύστημα των δύο σωμάτων:
$$ΣF_{x}=F-T_{1}-T_{2}=0$$
Άρα \(F=T_{1}+T_{2}=7,5N\)
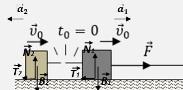
4.2 Από τη χρονική στιγμή \(t_{0}=0\) κατά την οποία κόπηκε το νήμα που συνέδεε τα δύο σώματα, η σταθερή δύναμη \(\vec{F}\) που κινούσε το σύστημα, ασκείται μόνο στο σώμα \(Σ_{1}\).
Εφαρμόζουμε τον θεμελιώδη νόμο της μηχανικής μόνο για το σώμα αυτό:
$$Σ_{1}: ΣF_{x}=F-T_{1}=m_{1}\cdot a_{1}$$ $$a_{1}=\dfrac{F-T_{1}}{m_{1}}=\dfrac{7,5-5}{2}\ \dfrac{m}{s^{2}}=1,25\ \dfrac{m}{s^{2}}$$
Το σώμα \(Σ_{2}\) στην οριζόντια διεύθυνση δέχεται μόνο την τριβή \(T_{2}\), η οποία το επιβραδύνει. Εφαρμόζουμε τον θεμελιώδη νόμο της μηχανικής για το σώμα αυτό:
$$Σ_{2} : ΣF_{x}'=-T_{2}=m_{2}\cdot a_{2}$$ $$a_{2}=\dfrac{-T_{2}}{m_{2}}=-\dfrac{2,5}{1}=-2,5\ \dfrac{m}{s^{2}}$$
το μέτρο της επιβράδυνσης του \(Σ_{2}\), είναι \(|a_{2}|=2,5\ \dfrac{m}{s^{2}}\)
4.3 Το σώμα \(Σ_{2}\) εκτελεί ευθύγραμμη ομαλά επιβραδυνόμενη κίνηση με αρχική ταχύτητα \(υ_{0}\), από τη χρονική στιγμή \(t_{0}=0\), μέχρι τη στιγμή \(t_{1}\) κατά την οποία ακινητοποιείται. Ισχύει:
$$υ=υ_{0}-|a_{2}|\cdot t_{1}=0$$ $$t_{1}=\dfrac{υ_{0}}{|a_{2}|}=\dfrac{2,5}{2,5}s=1 s$$
Σε αυτό το χρονικό διάστημα, μέχρι να ακινητοποιηθεί, έχει διανύσει:
$$S_{2}=υ_{0}\cdot t_{1}-\dfrac{1}{2}\cdot |a_{2}|\cdot t_{1}^{2}=(2,5\cdot 1-\dfrac{1}{2}\cdot 2,5\cdot 1)m=1,25 m$$
Στο ίδιο χρονικό διάστημα το σώμα \(Σ_{1}\) εκτελεί ευθύγραμμη ομαλά επιταχυνόμενη κίνηση με αρχική ταχύτητα \(υ_{0}\), από τη χρονική στιγμή \(t_{0}=0\) και μέχρι την στιγμή \(t_{1}\) διανύει διάστημα \(S_{1}\), για το οποίο ισχύει:
$$S_{1}=υ_{0}\cdot t_{1}+\dfrac{1}{2}\cdot a_{1}\cdot t_{1}^{2}=(2,5\cdot 1+\dfrac{1}{2}\cdot 1,25\cdot 1)m=3,125 m$$
Επειδή τη στιγμή \(t_{0}=0\) κατά την οποία κόπηκε το νήμα που τα συνέδεε, τα σώματα είχαν μεταξύ τους απόσταση \(l\) ίση με το μήκος του νήματος αυτού, τη στιγμή \(t_{1}\), κατά την οποία ακινητοποιείται το \(Σ_{2}\), η μεταξύ τους απόσταση είναι:
$$d=l+S_{1}-S_{2}=2\ m$$
4.4 Από τη στιγμή \(t_{0}=0\) που κόπηκε το νήμα, μέχρι το σώμα \(Σ_{1}\) να διανύσει διάστημα \(S=3\ m\), του έχει προσφερθεί ενέργεια μέσω του έργου της δύναμης \(\vec{F}\) η οποία το τραβάει:
$$E_{\text{πρ.}}=W_{F}=F\cdot S=7,5\cdot 3J=22,5 J$$
