Θέμα: 1805

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 5058 φορές Επικοινωνία
Μάθημα:	Γεωμετρία	Τάξη:	Α' Λυκείου
Κωδικός Θέματος:	1805	Θέμα:	4
Τελευταία Ενημέρωση:	01-Οκτ-2021	Ύλη:	3.2. 1ο Κριτήριο ισότητας τριγώνων 4.6. Άθροισμα γωνιών τριγώνου 5.2. Παραλληλόγραμμα
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Γεωμετρία
Θέμα:	4
Κωδικός Θέματος:	1805
Ύλη:	3.2. 1ο Κριτήριο ισότητας τριγώνων 4.6. Άθροισμα γωνιών τριγώνου 5.2. Παραλληλόγραμμα
Τελευταία Ενημέρωση: 01-Οκτ-2021
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ 4

Δίνεται παραλληλόγραμμο $Α Β Γ Δ$ και στην προέκταση της $Α Δ$ θεωρούμε σημείο $Ε$ τέτοιο ώστε $Δ Ε = Δ Γ$ ενώ στην προέκταση της $Α Β$ θεωρούμε σημείο θεωρούμε σημείο $Ζ$ τέτοιο ώστε $Β Ζ = Β Γ$ .

α) Να αποδείξετε ότι:
i. $\hat{B Γ Ζ} = \hat{Δ Γ Ε}$
(Μονάδες 10)
ii.τα σημεία $Ζ, Γ, Ε$ είναι συνευθειακά.
(Μονάδες 10)

β) Ένας μαθητής για να αποδείξει ότι τα σημεία $Ζ, Γ, Ε$ είναι συνευθειακά ανέπτυξε τον παρακάτω συλλογισμό. «Έχουμε:
$\hat{Β Γ Ζ} = \hat{Δ Ε Γ}$ (ως εντός εκτός και επι τα αυτά μέρη των παραλλήλων $Δ Ε$ και $Β Γ$ που τέμνονται από τη $Ζ Ε$ ) και
$\hat{Β Γ Δ} = Γ Δ Ε$ (ως εντός εναλλάξ των παραλλήλων $Δ Ε$ και $Β Γ$ που τέμνονται από την $Δ Γ$ ).
Όμως $\hat{Δ Γ Ε} + \hat{Γ Δ Ε} + \hat{Δ Ε Γ} = 180^{0}$ (ως άθροισμα των γωνιών του τριγώνου $Δ Ε Γ$ ). Άρα σύμφωνα με τα προηγούμενα: $\hat{Δ Γ Ε} + \hat{Γ Δ Ε} + \hat{Δ Ε Γ} = 180^{0}$ . Οπότε τα σημεία $Ζ, Γ, Ε$ είναι συνευθειακά.»
Όμως ο καθηγητής υπέδειξε ένα λάθος στο συλλογισμό αυτό. Να βρείτε το λάθος στο συγκεκριμένο συλλογισμό.
(Μονάδες 5)

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

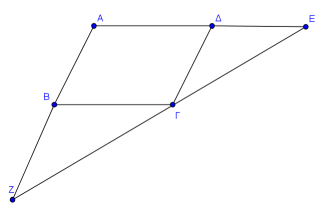
α)
i.Επειδή $B Z = B Γ$ , το τρίγωνο $Β Ζ Γ$ είναι ισοσκελές άρα $\hat{B Γ ̂ Z} = \hat{B Ζ ̂ Γ}$ . Από το άθροισμα γωνιών του τριγώνου $Β Γ Ζ$ έχουμε:

$\hat{Γ Β ̂ Ζ} + \hat{B Γ ̂ Z} + \hat{B Ζ ̂ Γ} = 180^{0} \Leftrightarrow 180^{0} - \hat{B} + 2 \hat{Β Γ Ζ} = 180^{0} \Leftrightarrow \hat{Β Γ ̂ Ζ} = \frac{\hat{B}}{2}$ .

Το τρίγωνο $Γ Δ Ε$ είναι ισοσκελές διότι $Δ Ε = Δ Γ$ οπότε $\hat{Δ Γ ̂ Ε} = \hat{Δ Ε ̂ Γ}$ .
Από το άθροισμα των γωνιών του τριγώνου $Γ Δ Ε$ , έχουμε:

$\hat{Δ Γ ̂ Ε} + \hat{Δ Ε ̂ Γ} + \hat{Ε Δ ̂ Γ} = 180^{0} \Leftrightarrow 2 \hat{Δ Γ ̂ Ε} + 180^{0} - \hat{Δ} = 180^{0} \Leftrightarrow \hat{Δ Γ ̂ Ε} = \frac{\hat{Δ}}{2}$

Επειδή $\hat{B} = \hat{Δ}$ , ως απέναντι γωνίες του παραλληλογράμμου, έχουμε $\hat{Β Γ ̂ Ζ} = \hat{Δ Γ ̂ Ε}$ .
ii. Η $\hat{Α Β ̂ Γ}$ είναι εξωτερική στο τρίγωνο $Β Ζ Γ$ οπότε $\hat{Α Β ̂ Γ} = \hat{Β Γ ̂ Ζ} + \hat{Β Γ ̂ Ζ} \Leftrightarrow \hat{Α Β ̂ Γ} = 2 \hat{Β Γ ̂ Ζ}$
Είναι: $\hat{Ζ Γ ̂ Ε} = \hat{Β Γ ̂ Ζ} + \hat{Β Γ ̂ Δ} + \hat{Δ Γ ̂ Ε} \Leftrightarrow \hat{Ζ Γ ̂ Ε} = 2 \hat{Β Γ ̂ Ζ} + \hat{Β Γ ̂ Δ} \Leftrightarrow \hat{Ζ Γ ̂ Ε} = \hat{Α Β ̂ Γ} + \hat{Β Γ ̂ Δ} \Leftrightarrow \hat{Ζ Γ ̂ Ε} = \hat{Α Β ̂ Γ} + \hat{Β Γ ̂ Δ} \Leftrightarrow \hat{Ζ Γ ̂ Ε} = 180^{0}$ διότι οι γωνίες $\hat{Α Β Γ}$ και $\hat{Β Γ Δ}$ είναι παραπληρωματικές. Άρα τα σημεία $Ζ, Γ, Ε$ είναι συνευθειακά.

β) Το λάθος οφείλεται στο συλλογισμό ότι χρησιμοποιήθηκε ως δεδομένο ότι τα $Ζ, Γ, Ε$ είναι συνευθειακά και αξιοποιήθηκε για να αποδείξουμε ότι οι γωνίες $\hat{Β Γ Ζ}$ και $\hat{Δ Ε Γ}$ είναι ίσες.