Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 10705 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 23135 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 24-Οκτ-2022 | Ύλη: | 2.2 Μηχανικά κύματα 4.10 Δύναμη Laplace (Λαπλάς) | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 23135 | ||
| Ύλη: | 2.2 Μηχανικά κύματα 4.10 Δύναμη Laplace (Λαπλάς) | ||
| Τελευταία Ενημέρωση: 24-Οκτ-2022 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
2.1. Μία πηγή αρμονικών κυμάτων βρίσκεται στην θέση \(x_{0}=0\) και την χρονική στιγμή \(t_{0}=0\) τίθεται σε ταλάντωση κάθετη στον οριζόντιο άξονα, κινούμενη αρχικά προς την θετική κατεύθυνση του άξονα \(y\). Την χρονική στιγμή \(t_{1}=4,5\ s\) το στιγμιότυπο του εγκάρσιου αρμονικού κύματος που προκαλεί η πηγή φαίνεται στο επόμενο σχήμα.
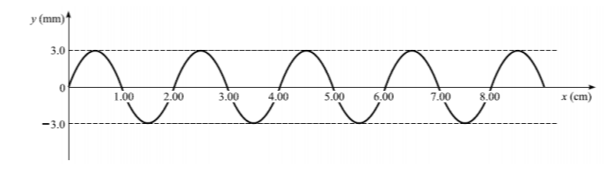
Η εξίσωση του αρμονικού κύματος που δημιουργεί η πηγή είναι
(α) \(y=0,003ημ2π(t -50x)\) (S.I.)
(β) \(y=0,003ημ2π(2t-50x)\) (S.I.)
(γ) \(y=0,003ημ2π(t -100x)\) (S.I.)
2.1.Α. Να επιλέξετε την ορθή απάντηση.
Μονάδες 4
2.1.B. Να αιτιολογήσετε την επιλογήσας.
Μονάδες 8
2.2. Στο εργαστήριο φυσικών επιστημών έχουμε δημιουργήσει την παρακάτω διάταξη με στόχο να υπολογίσουμε το μέτρο της έντασης του μαγνητικού πεδίου που δημιουργείται μεταξύ των πόλων ενός πεταλοειδή μαγνήτη. Το πεδίο αυτό θεωρείται ομογενές. Ευθύγραμμος μεταλλικός αγωγός \(ΚΛ\) με μήκος \(L=5\ cm\), μάζα \(m=1\ g\) και αντίσταση \(R=3\ Ω\) κρέμεται από δύο αγώγιμα σύρματα \(ΑΚ\) και \(ΛΓ\) αμελητέας μάζας. Οι δυνάμεις που ασκούν τα σύρματα \(ΑΚ\) και \(ΛΓ\) στον μεταλλικό αγωγό θεωρούνται αμελητέες. Τα σημεία \(Α\) και \(Γ\) συνδέονται με γεννήτρια του εργαστηρίου, στην οθόνη της οποίας μπορούμε να δούμε την τάση εξόδου.
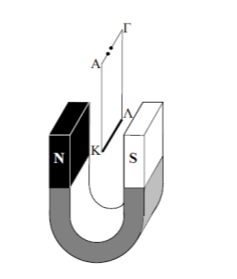
Ο αγωγός \(ΚΛ\) τοποθετείται εξ ολοκλήρου στο εσωτερικό του μαγνητικού πεδίου που δημιουργείται από τον πεταλοειδή μαγνήτη. Ρυθμίζουμε την τάση (τιμή και πολικότητα) ώστε ο αγωγός να ισορροπήσει σε οριζόντια θέση, κάθετα στις δυναμικές γραμμές του πεδίου και παρατηρούμε ότι η ένδειξη στην οθόνη της γεννήτριας είναι \(V=20\ V\). Αν η επιτάχυνση της βαρύτητας έχει μέτρο \(g=10\ \dfrac{m}{s^{2}}\) και το μαγνητικό πεδίο της Γης θεωρείται αμελητέο, τότε το μέτρο της έντασης του μαγνητικού πεδίου είναι:
(α) \(Β=0,02\ Τ\)
(β) \(Β=0,03\ Τ\)
(γ) \(Β=0,04\ Τ\)
2.2.Α. Να επιλέξετε την ορθή απάντηση.
Μονάδες 4
2.2.B. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 9
ΘΕΜΑ 2
2.1.
2.1.Α. Σωστή απάντηση η (α)
Μονάδες 4
2.1.B.
Το κύμα διαδίδεται προς την θετική κατεύθυνση του οριζόντιου άξονα και η ταλάντωση που εκτελεί η πηγή έχει αρχική φάση \(φ=0\) γιατί αρχικά κινείται προς την θετική κατεύθυνση του κατακόρυφου άξονα. Με βάση αυτά τα δεδομένα η εξίσωση του αρμονικού κύματος θα έχει μορφή \(y=Aημ2π(\dfrac{t}{Τ}-\dfrac{x}{λ})\).
Παρατηρώντας το στιγμιότυπο του κύματος βρίσκουμε ότι το πλάτος του είναι \(Α=3\ mm\). Επίσης, βλέπουμε ότι η απόσταση \(x_{1}=9\ cm\) στην οποία έχει διαδοθεί το κύμα την χρονική στιγμή \(t_{1}\) αντιστοιχεί σε \(4,5\) μήκη κύματος, δηλαδή
$$x_{1}=4,5λ $$ $$\Rightarrow λ=\dfrac{x_{1}}{4,5}=\dfrac{9}{4,5}\ cm=2\ cm$$
Η ταχύτητα διάδοσης του κύματος είναι
$$υ=\dfrac{x_{1}}{t_{1}}=\dfrac{9}{4,5}\ \dfrac{cm}{s}=2\ \dfrac{cm}{s}$$
Από την θεμελιώδη εξίσωση της κυματικής, η περίοδος του αρμονικού κύματος είναι
$$υ=\dfrac{λ}{Τ} $$ $$\Rightarrow Τ=\dfrac{λ}{υ}=\dfrac{2}{2}\ s=1\ s$$
Συνεπώς, το αρμονικό κύμα έχει εξίσωση
$$y=Aημ2π(\dfrac{t}{Τ}-\dfrac{x}{λ})$$ $$\Rightarrow y=0,003ημ2π(\dfrac{t}{1}-\dfrac{x}{0,02})$$ $$\Leftrightarrow y=0,003ημ2π(t-50x) \ \ \ \ \text{(S.I.)}$$
Μονάδες 8
2.2.
2.2.A. Σωστή απάντηση η (β)
Μονάδες 4
2.2.B.
Στο εσωτερικό του ομογενούς μαγνητικού πεδίου που δημιουργεί ο πεταλοειδής μαγνήτης, ο μεταλλικός αγωγός \(ΚΛ\) δέχεται δύο δυνάμεις. Η μία δύναμη είναι το βάρος του και έχει μέτρο \(mg\). Η άλλη δύναμη που δέχεται είναι η δύναμη Laplace, γιατί διαρρέεται από ηλεκτρικό ρεύμα έντασης \(I=\dfrac{V}{R}\), με φορά από το \(Λ\) προς το \(Κ\) και βρίσκεται στο εσωτερικό ομογενούς μαγνητικού πεδίου. Η δύναμη αυτή έχει μέτρο \(F_{L}=BIL\) γιατί ο αγωγός είναι κάθετος στην ένταση του μαγνητικού πεδίου.
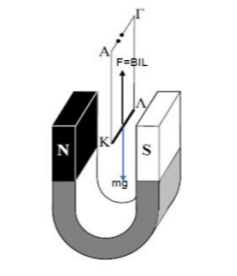
Όταν ο αγωγός \(ΚΛ\) ισορροπήσει αυτές οι δύο δυνάμεις είναι αντίθετες, όπως φαίνεται στο σχήμα. Τότε ισχύει
$$F_{L}=mg$$ $$\Leftrightarrow BIL=mg$$ $$\Rightarrow B\dfrac{V}{R}L=mg$$ $$\begin{align} \Leftrightarrow B &=\dfrac{mgR}{VL} \\ &=\dfrac{10^{-3}\cdot 10\cdot 3}{20\cdot 5\cdot 10^{-2}}\ T \\ &=3\cdot 10^{-2}\ T \\ &=0,03\ T \end{align}$$
Μονάδες 9