Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 20868 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 23247 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 29-Απρ-2023 | Ύλη: | 5.2 Κρούσεις 1.3 Απλή αρμονική ταλάντωση | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 23247 | ||
| Ύλη: | 5.2 Κρούσεις 1.3 Απλή αρμονική ταλάντωση | ||
| Τελευταία Ενημέρωση: 29-Απρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Ένα βλήμα μάζας

Στο συσσωμάτωμα ασκείται, επίσης, δύναμη αντίστασης στην κίνησή του της μορφής
4.1. Την ταχύτητα του συσσωματώματος αμέσως μετά την κρούση.
Μονάδες 7
4. 2. Την μέγιστη συσπείρωση του ελατηρίου.
Μονάδες 9
Μόλις το συσσωμάτωμα βρεθεί στη θέση μέγιστης συσπείρωσης του ελατηρίου, καταργείται η δύναμη αντίστασης και το σύστημα εκτελεί απλή αρμονική ταλάντωση, με θετική φορά προς τα δεξιά.
4. 3. Να γράψετε τις εξισώσεις:
- της απομάκρυνσης ως προς τον χρόνο.
- της δύναμης επαναφοράς ως προς την απομάκρυνση.
Μονάδες 9
ΘΕΜΑ 4
4.1. Κατά την διάρκεια της κρούσης το σύστημα θεωρείται μονωμένο και ισχύει η Α.Δ.Ο.:
Μονάδες 7
4. 2. Αμέσως μετά την κρούση το συσσωμάτωμα εκτελεί επιβραδυνόμενη κίνηση, λόγω της δύναμης του ελατηρίου και της δύναμης αντίστασης που του ασκούνται, όπως φαίνεται στο σχήμα:
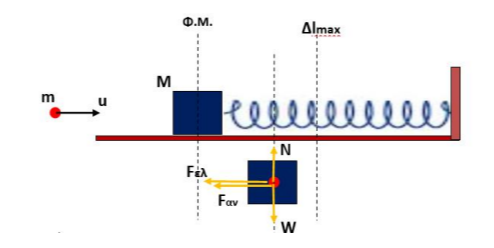
Αρχικά υπολογίζουμε το μέτρο της δύναμης αντίστασης:
Εφαρμόζουμε Θ.Μ.Κ.Ε. για το συσσωμάτωμα, από την θέση Φ.Μ. του ελατηρίου όπου έγινε η κρούση έως την θέση που σταματά στιγμιαία.
Η τιμή
Η αρνητική τιμή που προκύπτει αντιστοιχεί στην μέγιστη επιμήκυνση του ελατηρίου η οποία δεν ζητείται.
Μονάδες 9
4. 3. Η εξίσωση ταλάντωσης είναι της μορφής :
Για το πλάτος της ταλάντωσης είναι:
Επίσης ισχύει:
Και για την αρχική φάση:
Οπότε η ζητούμενη εξίσωση ταλάντωσης θα είναι:
Η σχέση της συνισταμένης δύναμης στον ταλαντωτή με την απομάκρυνση είναι:
Μονάδες 9
