Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
Έναρξη από 2 Σεπτεμβρίου
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 7699 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Οικονομία | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 29024 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 19-Μαρ-2024 | Ύλη: | Κεφάλαιο 1: Βασικές Οικονομικές Έννοιες | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Οικονομία | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 29024 | ||
| Ύλη: | Κεφάλαιο 1: Βασικές Οικονομικές Έννοιες | ||
| Τελευταία Ενημέρωση: 19-Μαρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4ο
Μία οικονομία, σε ένα έτος \(t\), παράγει δύο αγαθά \(Χ\) και \(Ψ\) και απασχολεί όλους τους παραγωγικούς συντελεστές πλήρως και αποδοτικά (ορθολογικά) με δεδομένη τεχνολογία, όπως στον παρακάτω πίνακα.
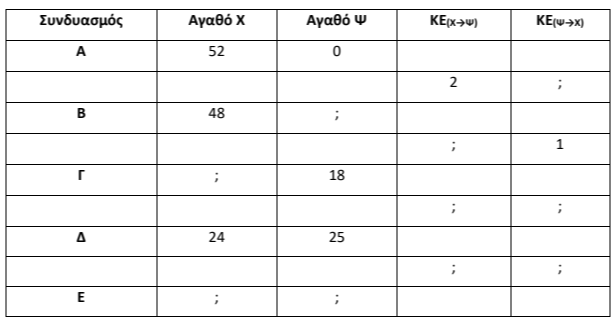
α) Να μεταφέρετε τον πίνακα στο τετράδιό σας και κάνοντας τους κατάλληλους υπολογισμούς, να
συμπληρώσετε τα δέκα (\(10\)) κενά του πίνακα με τα ερωτηματικά. Ισχύει ότι, όταν όλοι οι παραγωγικοί συντελεστές απασχολούνται στην παραγωγή του αγαθού \(Ψ\) (συνδυασμός \(Ε\)), τότε η οικονομία παράγει \(31\) μονάδες του αγαθού \(Ψ\).
(Μονάδες 5)
β) Να εξετάσετε υπολογιστικά, εάν ο συνδυασμός \(Χ = 40\) και \(Ψ = 15\) βρίσκεται επί, αριστερά ή δεξιά της Καμπύλης Παραγωγικών Δυνατοτήτων (Κ.Π.Δ.).
(Μονάδες 5)
γ) Να υπολογίσετε πόσες μονάδες από το αγαθό \(Ψ\) θα θυσιαστούν, προκειμένου να παραχθούν οι πρώτες \(20\) μονάδες του αγαθού \(Χ\);
(Μονάδες 5)
δ) Να υπολογίσετε πόσες μονάδες από το αγαθό \(Ψ\) θα θυσιαστούν, προκειμένου να παραχθούν οι τελευταίες \(20\) μονάδες του αγαθού \(Χ\);
(Μονάδες 5)
ε) Ας υποθέσουμε ότι η οικονομία παράγει τον συνδυασμό \(Δ\). Εάν η τιμή πώλησης του αγαθού \(Χ\) είναι \(15\) ευρώ και η τιμή πώλησης του αγαθού \(Ψ\) είναι \(8\) ευρώ, να βρεθεί το ονομαστικό Ακαθάριστο Εγχώριο Προϊόν (Α.Ε.Π.) της οικονομίας στο έτος \(t\).
(Μονάδες 5)
ΑΠΑΝΤΗΣΗ ΘΕΜΑΤΟΣ 4ου
α) Για το συνδυασμό \(Α-Β\) έχουμε:
$$ΚΕ_{Χ\rightarrow Ψ}=2 $$ $$\Leftrightarrow \dfrac{Δ_{Ψ}}{Δ_{Χ}}=2 $$ $$\Leftrightarrow \dfrac{Ψ_{Β}-0}{52-48}=2 $$ $$\Leftrightarrow \dfrac{Ψ_{Β}}{4}=2 $$ $$\Rightarrow Ψ_{Β}=8\ \text{μονάδες προϊόντος}$$
$$ΚΕ_{Ψ\rightarrow Χ}=\dfrac{Δ_{Χ}}{Δ_{Ψ}}$$ $$=\dfrac{52-48}{8-0}$$ $$=\dfrac{4}{8}=\dfrac{1}{2}$$ $$=0,5\ \text{μονάδες αγαθού Χ}$$
Για το συνδυασμό \(Β-Γ\) έχουμε:
$$ΚΕ_{Ψ\rightarrow Χ}=1 $$ $$\Leftrightarrow \dfrac{Δ_{Χ}}{Δ_{Ψ}}=1 $$ $$\Leftrightarrow \dfrac{48-Χ_{Γ}}{18-8}=1 $$ $$\Leftrightarrow \dfrac{48-Χ_{Γ}}{10}=1 $$ $$\Leftrightarrow 48-Χ_{Γ}=10 $$ $$\Rightarrow Χ_{Γ}=38\ \text{μονάδες προϊόντος}$$
$$ΚΕ_{Χ\rightarrow Ψ}=\dfrac{Δ_{Ψ}}{Δ_{Χ}}$$ $$=\dfrac{18-8}{48-38}=\dfrac{10}{10}$$ $$=1\ \text{μονάδα αγαθού Ψ}$$
Για το συνδυασμό \(Γ-Δ\) έχουμε:
$$ΚΕ_{Χ\rightarrow Ψ}=\dfrac{Δ_{Ψ}}{Δ_{Χ}}$$ $$=\dfrac{25-18}{38-24}$$ $$=\dfrac{7}{14}=\dfrac{1}{2}$$ $$=0,5\ \text{μονάδες αγαθού Ψ}$$
$$ΚΕ_{Ψ\rightarrow Χ}=\dfrac{Δ_{Χ}}{Δ_{Ψ}}$$ $$=\dfrac{38-24}{25-18}=\dfrac{14}{7}$$ $$=2\ \text{μονάδες αγαθού Χ}$$
Για το συνδυασμό \(Δ-Ε\) έχουμε:
Επειδή όλοι οι παραγωγικοί συντελεστές απασχολούνται στην παραγωγή του αγαθού \(Ψ\) στον συνδυασμό \(Ε\), τότε η οικονομία παράγει \(31\) μονάδες του αγαθού \(Ψ\) και \(0\) μονάδες του αγαθού \(Χ\). Δηλαδή \(Χ_Ε = 0\) και \(Ψ_Ε = 31\).
$$ΚΕ_{Χ\rightarrow Ψ}=\dfrac{Δ_{Ψ}}{Δ_{Χ}}$$ $$=\dfrac{31-25}{24-0}$$ $$=\dfrac{6}{24}=\dfrac{1}{4}$$ $$=0,25\ \text{μονάδες αγαθού Ψ}$$
$$ΚΕ_{Ψ\rightarrow Χ}=\dfrac{Δ_{Χ}}{Δ_{Ψ}}$$ $$=\dfrac{24-0}{31-25}=\dfrac{24}{6}$$ $$=4\ \text{μονάδες αγαθού Χ}$$
Ο πίνακας παραγωγικών δυνατοτήτων της οικονομίας συμπληρωμένος είναι ο εξής:
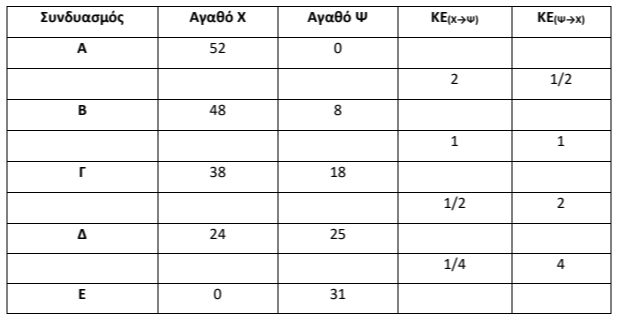
(Μονάδες 5)
β) Η παραγωγή των \(40\) μονάδων του αγαθού \(Χ\) βρίσκεται ανάμεσα στους συνδυασμούς \(Β\) και \(Γ\), όπου το κόστος ευκαιρίας του αγαθού \(Χ\) είναι σταθερό και ίσο με \(1\) για όλους τους συνδυασμούς που βρίσκονται μεταξύ των συνδυασμών \(Β\) και \(Γ\). Κατασκευάζουμε ένα νέο πίνακα, παρεμβάλλοντας τον συνδυασμό \(Β'\) με την ποσότητα \(40\) μονάδων του αγαθού \(Χ\) και αναζητούμε τη μέγιστη ποσότητα του αγαθού \(Ψ\):
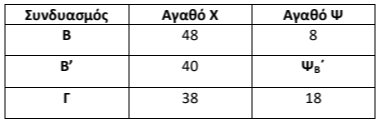
Στη συνέχεια με τη βοήθεια του κόστους ευκαιρίας βρίσκουμε το \(ΨΒ'\) στον συνδυασμό \(Β'-Γ\):
$$ΚΕ_{Χ\rightarrow Ψ}=1 $$ $$\Leftrightarrow \dfrac{Δ_{Ψ}}{Δ_{Χ}}=1 $$ $$\Leftrightarrow \dfrac{18-Ψ_{Β'}}{40-38}=1 $$ $$\Leftrightarrow \dfrac{18-Ψ_{Β'}}{2}=1 $$ $$\Leftrightarrow 18-Ψ_{Β'}=2 $$ $$\Rightarrow Ψ_{Β'}=16\ \text{μονάδες προϊόντος}$$
Δηλαδή, με δεδομένη την παραγωγή \(40\) μονάδων του αγαθού \(Χ\), η μέγιστη ποσότητα του αγαθού \(Ψ\) που μπορεί να παράγει η οικονομία είναι \(16\) μονάδες.
Αυτό σημαίνει ότι, οι \(15\) μονάδες \(Ψ\) του ζητούμενου συνδυασμού μπορούν να παραχθούν με βάση τους δεδομένους παραγωγικούς συντελεστές που διαθέτει η συγκεκριμένη οικονομία, αλλά δεν είναι οι μέγιστες.
Συνεπώς, ο ζητούμενος συνδυασμός (\(Χ = 40\), \(Ψ = 15\)) είναι εφικτός, αλλά η οικονομία υποαπασχολεί μέρος των παραγωγικών συντελεστών που διαθέτει. Διαγραμματικά, ο ζητούμενος συνδυασμός βρίσκεται αριστερά της Καμπύλης Παραγωγικών Δυνατοτήτων.
(Μονάδες 5)
γ) Οι πρώτες \(20\) μονάδες του αγαθού \(Χ\) παράγονται από τις \(0\) έως τις \(20\) μονάδες.
Η παραγωγή των \(20\) μονάδων του αγαθού \(Χ\) βρίσκεται ανάμεσα στους συνδυασμούς \(Δ\) και \(Ε\), όπου το κόστος ευκαιρίας του αγαθού \(Χ\) είναι σταθερό και ίσο με \(1/4\) για όλους τους συνδυασμούς που βρίσκονται μεταξύ των συνδυασμών \(Δ\) και \(Ε\). Κατασκευάζουμε ένα νέο πίνακα, παρεμβάλλοντας τον συνδυασμό \(Δ'\) με την ποσότητα \(20\) μονάδων του αγαθού \(Χ\) και αναζητούμε τη μέγιστη ποσότητα του αγαθού \(Ψ\):
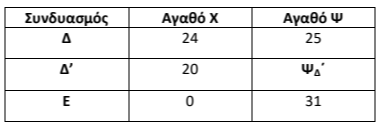
Στη συνέχεια με τη βοήθεια του κόστους ευκαιρίας βρίσκουμε το \(Ψ_Β'\) στον συνδυασμό \(Β'-Γ\):
$$ΚΕ_{Χ\rightarrow Ψ}=\dfrac{1}{4} $$ $$\Leftrightarrow \dfrac{Δ_{Ψ}}{Δ_{Χ}}=\dfrac{1}{4} $$ $$\Leftrightarrow \dfrac{31-Ψ_{Δ'}}{20-0}=\dfrac{1}{4} $$ $$\Leftrightarrow \dfrac{31-Ψ_{Δ'}}{20}=\dfrac{1}{4} $$ $$\Leftrightarrow 31-Ψ_{Δ'}=\dfrac{20}{4} $$ $$\Leftrightarrow 31-Ψ_{Δ'}=5 $$ $$\Rightarrow Ψ_{Δ'}=26\ \text{μονάδες προϊόντος}$$
Δηλαδή, με δεδομένη την παραγωγή \(20\) μονάδων του αγαθού \(Χ\), η μέγιστη ποσότητα του αγαθού \(Ψ\) που μπορεί να παράγει η οικονομία είναι \(26\) μονάδες.
Άρα για να παραχθούν οι πρώτες \(20\) μονάδες του αγαθού \(Χ\), πρέπει να θυσιαστούν \(31 - 26 = 5\) μονάδες του αγαθού \(Ψ\).
(Μονάδες 5)
δ) Οι τελευταίες \(20\) μονάδες του αγαθού \(Χ\) παράγονται από τις \(32\) έως τις \(52\) μονάδες.
Η παραγωγή των \(32\) μονάδων του αγαθού \(Χ\) βρίσκεται ανάμεσα στους συνδυασμούς \(Γ\) και \(Δ\), όπου το κόστος ευκαιρίας του αγαθού \(Χ\) είναι σταθερό και ίσο με \(0,5\) για όλους τους συνδυασμούς που βρίσκονται μεταξύ των συνδυασμών \(Γ\) και \(Δ\). Κατασκευάζουμε ένα νέο πίνακα, παρεμβάλλοντας τον συνδυασμό \(Γ'\) με την ποσότητα \(32\) μονάδων του αγαθού \(Χ\) και αναζητούμε τη μέγιστη ποσότητα του αγαθού \(Ψ\):
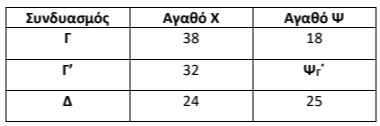
Στη συνέχεια με τη βοήθεια του κόστους ευκαιρίας βρίσκουμε το \(Ψ_Γ'\) στον συνδυασμό \(Γ'-Δ\):
$$ΚΕ_{Χ\rightarrow Ψ}=0,5 $$ $$\Leftrightarrow \dfrac{Δ_{Ψ}}{Δ_{Χ}}=0,5 $$ $$\Leftrightarrow \dfrac{25-Ψ_{Γ'}}{32-24}=0,5 $$ $$\Leftrightarrow \dfrac{25-Ψ_{Γ'}}{8}=0,5 $$ $$\Leftrightarrow 25-Ψ_{Γ'}=4 $$ $$\Rightarrow Ψ_{Γ'}=21\ \text{μονάδες προϊόντος}$$
Άρα, με δεδομένη την παραγωγή \(32\) μονάδων του αγαθού \(Χ\), η μέγιστη ποσότητα του αγαθού \(Ψ\) που μπορεί να παράγει η οικονομία είναι \(21\) μονάδες.
Άρα για να παραχθούν οι τελευταίες \(20\) μονάδες του αγαθού \(Χ\), πρέπει να θυσιαστούν \(21 – 0 = 21\) μονάδες του αγαθού \(Ψ\).
(Μονάδες 5)
ε) Στον συνδυασμό \(Δ\), η οικονομία το έτος \(t\) παράγει \(Q_X = 24\) μονάδες του αγαθού \(Χ\) με τιμή πώλησης \(P_Χ = 15\) ευρώ και \(Q_Ψ = 25\) μονάδες του αγαθού \(Ψ\) με τιμή πώλησης \(P_Ψ = 8\) ευρώ.
Τα ονομαστικό Α.Ε.Π. το έτος \(t\) είναι:
$$\text{Α.Ε.Π.}_{\text{ΟΝΟΜΑΣΤΙΚΟ}(t)}=[P_{Χ(t)}\cdot Q_{Χ(t)}]+[P_{Ψ(t)}\cdot Q_{Ψ(t)}]$$ $$=(15\cdot 24)+(8\cdot 25)$$ $$=360+200=560\ \text{ευρώ}$$
(Μονάδες 5)
