Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 5543 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 34116 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 21-Μαΐ-2023 | Ύλη: | 2.4 Συμβολή δύο κυμάτων στην επιφάνεια υγρού | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 34116 | ||
| Ύλη: | 2.4 Συμβολή δύο κυμάτων στην επιφάνεια υγρού | ||
| Τελευταία Ενημέρωση: 21-Μαΐ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Δύο σύγχρονες πηγές αρμονικών κυμάτων
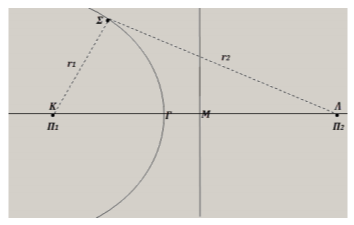
Οι δύο πηγές ξεκινούν ταυτόχρονα τις αρμονικές ταλαντώσεις τους, τη χρονική στιγμή
Να υποθέσετε ότι για τις διαστάσεις αυτού του πειράματος, τα κύματα από τις δύο πηγές φτάνουν στο
Να υπολογίσετε:
4.1. το μήκος κύματος, των κυμάτων που παράγουν οι δύο πηγές, στην επιφάνεια του υγρού,
Μονάδες 6
4.2. τις αποστάσεις
Μονάδες 6
Το σημείο
4.3. Να υπολογίσετε την απόσταση
Μονάδες 6
4.4. Αν δίνεται ότι τα ευθύγραμμα τμήματα
Μονάδες 7
ΘΕΜΑ 4
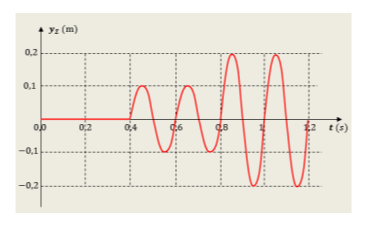
4.1. Από το δεδομένο διάγραμμα απομάκρυνσης από τη θέση ισορροπίας του σε συνάρτηση με το χρόνο, για την ταλάντωση που εκτελεί το σημείο
Έτσι μπορούμε να γνωρίζουμε και τη συχνότητα των ταλαντώσεων, αλλά και το μήκος κύματος των κυμάτων που διαδίδονται από τις δύο πηγές, στην ελεύθερη επιφάνεια του υγρού:
Μονάδες 6
4.2. Το κύμα της πηγής
Το κύμα της πηγής
Μονάδες 6
4.3. Το σημείο
Μονάδες 6
4. 4. Εφαρμόζουμε το πυθαγόρειο θεώρημα στο ορθογώνιο τρίγωνο
Έστω ένα σημείο
Για την απόσταση
που σημαίνει:
Δηλαδή
Μονάδες 7
