Τράπεζα Θεμάτων

www.trapeza-thematon.gr

Τύπος Σχολείου:	Γενικό Λύκειο	Τάξη:	Α' Λυκείου
Μάθημα:	Φυσική	Θέμα:	4
Κωδικός Θέματος:	11648	Ύλη:

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Φυσική
Θέμα:	4
Κωδικός Θέματος:	11648
Ύλη:
Τελευταία Ενημέρωση: 15-Απρ-2024

ΘΕΜΑ Δ
Μία παλέτα με τούβλα μάζας $m = 400 k g$ ανυψώνεται κατακόρυφα με τη βοήθεια ενός γερανού κατά $10 m$ πάνω από το έδαφος. Ο γερανός ασκεί στην παλέτα κατακόρυφη δύναμη με φορά προς τα πάνω, το μέτρο της οποίας έχει τέτοια τιμή ώστε η παλέτα ξεκινώντας από την ηρεμία αρχικά να επιταχύνεται με σταθερή επιτάχυνση για χρονική διάρκεια ίση με $5 s$ και να φτάνει σε ύψος $5 m$ από το έδαφος και στη συνέχεια να επιβραδύνεται ομαλά μέχρι να σταματήσει σε ύψος 10 m πάνω από το έδαφος.
Δίνεται η επιτάχυνση της βαρύτητας $g = 10 \frac{m}{s^{2}}$ και ότι η αντίσταση του αέρα θεωρείται αμελητέα.
Να υπολογίσετε:
Δ1) το μέτρο της επιτάχυνσης της παλέτας στα πρώτα $5 s$ της κίνησης, καθώς και το μέτρο της ταχύτητας που αποκτά στο τέλος της επιταχυνόμενης κίνησης,
Μονάδες 6

Δ2) το μέτρο της δύναμης που ασκεί ο γερανός στην παλέτα κατά τη διάρκεια της επιταχυνόμενης κίνησης,
Μονάδες 6

Δ3) το μέτρο της δύναμης που ασκεί ο γερανός στην παλέτα κατά τη διάρκεια της επιβραδυνόμενης κίνησης,
Μονάδες 7

Δ4) τη μέση ισχύ του γερανού κατά τη διάρκεια της ανόδου της παλέτας.
Μονάδες 6

Απάντηση Θέματος:

Ενδεικτική Λύση
Δ1)
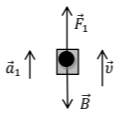
Έστω ${\vec{F}}_{1}$ η δύναμη που ασκεί ο γερανός στο κιβώτιο, $\vec{Β}$ το βάρος του και ${\vec{α}}_{1}$ η επιτάχυνση κατά την ομαλά επιταχυνόμενη κίνηση του. Τα ζητούμενα υπολογίζονται εφαρμόζοντας την εξίσωση της μετατόπισης και την εξίσωση της ταχύτητας αντίστοιχα:

$Δ y = \frac{1}{2} a_{1} t_{1}^{2}$ $5 = \frac{1}{2} a_{1} \cdot 25$ $a_{1} = 0, 4 \frac{m}{s^{2}}$ $υ_{1} = α_{1} \cdot t_{1}$ $υ_{1} = 2 \frac{m}{s}$

Δ2) Εφαρμόζουμε το 2ο νόμο του Newton λαμβάνοντας ως θετική τη φορά της επιτάχυνσης:

$Σ \vec{F} = m \cdot \vec{a}$ $F_{1} - B = m \cdot a_{1}$ $F_{1} = 4160 N$

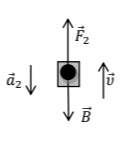
Δ3) Έστω τώρα ${\vec{F}}_{2}$ η δύναμη που ασκεί ο γερανός στο κιβώτιο και ${\vec{α}}_{2}$ η επιβράδυνση κατά την ομαλά επιβραδυνόμενη κίνηση του.

Εφαρμόζουμε Θεώρημα Μεταβολής της Κινητικής Ενέργειας – Έργου (ΘΜΚΕ) για τη μετατόπιση του κιβωτίου κατά $5 m$ στην επιβραδυνόμενη κίνηση του:

$Κ_{τελ} - Κ_{αρχ} = W_{F} + W_{Β}$ $0 - \frac{1}{2} m \cdot υ_{1}^{2} = F_{2} \cdot Δ y - m \cdot g \cdot Δ y$ $F_{2} = 3.840 N$

Δ4) Εφαρμόζουμε το Θεώρημα Μεταβολής της Κινητικής Ενέργειας – Έργου
(ΘΜΚΕ) για τη συνολική μετατόπιση του κιβωτίου:

$Κ_{τελ} - Κ_{αρχ} = W_{F} + W_{Β}$ $0 - 0 = W_{F} + W_{Β}$ $W_{F} = - W_{Β}$

Εφαρμόζουμε το 2ο νόμο του Newton στην ομαλά επιβραδυνόμενη κίνηση λαμβάνοντας ως θετική τη φορά της επιβράδυνσης:

$Σ \vec{F} = m \vec{a}$ $B - F_{2} = m α_{2}$ $α_{2} = 0, 4 \frac{m}{s}$

Και από την εξίσωση της ταχύτητας με $υ = 0$ υπολογίζουμε τη χρονική διάρκεια της επιβραδυνόμενης κίνησης:

$υ = υ_{1} - α_{2} \cdot t_{2}$ $Δ t_{2} = 5 s$

Και τελικά υπολογίζουμε την μέση ισχύ:

$\bar{P} = \frac{W_{F}}{Δ_{t ο λ}}$ $\bar{P} = \frac{| W_{B} |}{Δ t_{1} + Δ t_{2}}$ $\bar{P} = 4.000 W$

Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).