Τράπεζα Θεμάτων

www.trapeza-thematon.gr

Τύπος Σχολείου:	Γενικό Λύκειο	Τάξη:	Α' Λυκείου
Μάθημα:	Φυσική	Θέμα:	4
Κωδικός Θέματος:	11664	Ύλη:	Χωρίς Αντιστοίχιση Ύλης

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Φυσική
Θέμα:	4
Κωδικός Θέματος:	11664
Ύλη:	Χωρίς Αντιστοίχιση Ύλης
Τελευταία Ενημέρωση: 24-Οκτ-2024

ΘΕΜΑ Δ

Μικρό σώμα μάζας $m = 400 g$ βρίσκεται αρχικά ακίνητο σε οριζόντιο επίπεδο με το οποίο εμφανίζει συντελεστή τριβής ολίσθησης $μ = 0, 25$ . Τη χρονική στιγμή $t = 0 s$ ασκείται στο σώμα οριζόντια σταθερή δύναμη $\vec{F}$ μέτρου ίσου με $5 Ν$ , μέχρι τη χρονική στιγμή $t_{1} = 5 s$ , όπου καταργείται.

Δίνεται ότι η επιτάχυνση της βαρύτητας είναι $g = 10 \frac{m}{S^{2}}$ και ότι η επίδραση του αέρα θεωρείται αμελητέα.

Για το χρονικό διάστημα που ασκείται η δύναμη:
Δ1) να υπολογίσετε το μέτρο της επιτάχυνσης με την οποία κινείται το σώμα.
Μονάδες 7

Δ2) να σχεδιάσετε σε βαθμολογημένους άξονες το διάγραμμα ταχύτητας - χρόνου $(υ - t)$ .
Μονάδες 5

Δ3) να υπολογίσετε το έργο της δύναμης $\vec{F}$ .
Μονάδες 6

Δ4) να υπολογίσετε το μέσο ρυθμό με τον οποίο η προσφερόμενη στο σώμα ενέργεια μετατρέπεται σε θερμική.
Μονάδες 7

Απάντηση Θέματος:

Ενδεικτική Λύση
Δ1) Στο σχήμα έχουν σχεδιαστεί οι δυνάμεις που ασκούνται στο σώμα από τη χρονική στιγμή $t_{0} = 0 s$ έως τη χρονική στιγμή $t_{1} = 5 s$ .

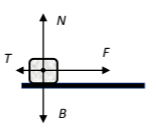
Από το 2ο νόμο του Νεύτωνα έχουμε:

$Σ F_{x} = m α$ $\Rightarrow F - T = m α (1)$

$Σ F_{y} = 0$ $\Rightarrow N = B (2)$

Αλλά

$T = μ N \Rightarrow T = μ B$ $\Rightarrow T = μ m g$ $\Rightarrow T = 1 N, (3)$

Συνδυάζοντας τις σχέσεις (1) και (3) έχουμε τελικά:

$α = 10 \frac{m}{s^{2}}$

**Δ2)** Από τη σχέση

u = u_{0} + a t

με

u_{0} = 0

σχεδιάζετε το διάγραμμα ταχύτητας-χρόνου

(u - t)

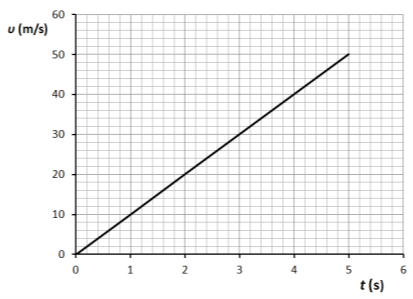
Δ3) Από το προηγούμενο διάγραμμα η μετατόπιση του σώματος είναι:

$Δ x = \frac{50 \cdot 5}{2} = 125 m .$

To έργο της δύναμης $\vec{F}$ είναι:

$W_{F} = F \cdot Δ x = 625 J$

Δ4) Ο μέσος ρυθμός με τον οποίο η προσφερόμενη στο σώμα ενέργεια μετατρέπεται σε θερμική, μέσω του έργου της τριβής είναι:

$\frac{Δ Q}{Δ t} = \frac{| W_{T} |}{Δ t}$ $\Rightarrow \frac{Δ Q}{Δ t} = \frac{| - 1 \cdot 125 |}{5}$ $\Rightarrow \frac{Δ Q}{Δ t} = 25 \frac{J}{s}$

Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).