Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Α' Λυκείου |
|---|---|---|---|
| Μάθημα: | Φυσική | Θέμα: | 4 |
| Κωδικός Θέματος: | 11673 | Ύλη: | Χωρίς Αντιστοίχιση Ύλης |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Α' Λυκείου |
| Μάθημα: | Φυσική |
| Θέμα: | 4 |
| Κωδικός Θέματος: | 11673 |
| Ύλη: | Χωρίς Αντιστοίχιση Ύλης |
| Τελευταία Ενημέρωση: 24-Οκτ-2024 | |
ΘΕΜΑ Δ
Μεταλλικός κύβος μάζας \(m\) κινείται ευθύγραμμα πάνω σε λείο οριζόντιο δάπεδο έχοντας τη χρονική στιγμή \(t = 0 s\) ταχύτητα μέτρου \(4 m/s\). Στον κύβο ασκείται τη χρονική στιγμή \(t = 0 s\) δύναμη, ίδιας διεύθυνσης με τη ταχύτητα του. Η τιμή της δύναμης σε συνάρτηση με το χρόνο, για το χρονικό διάστημα φαίνεται στο παρακάτω διάγραμμα.
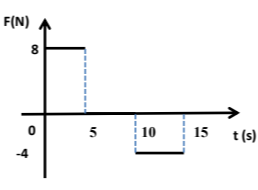
Η αντίσταση του αέρα θεωρείται αμελητέα.
Τη χρονική στιγμή \(t_1 = 5 s\) ο κύβος έχει αποκτήσει ταχύτητα μέτρου \(υ=14\dfrac{m}{s}\).
Δ1) Να χαρακτηρίσετε τη κίνηση που εκτελεί το σώμα στο χρονικό διάστημα \(0 → 5 s\) και να υπολογίσετε το μέτρο της επιτάχυνσης του.
Μονάδες 6
Δ2) Να υπολογίσετε τη μάζα του κύβου.
Μονάδες 6
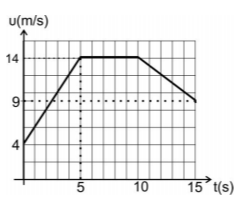
Δ3) Να παραστήσετε γραφικά το μέτρο της ταχύτητας του κύβου, σε συνάρτηση με το χρόνο σε σύστημα βαθμολογημένων αξόνων για το χρονικό διάστημα \(0\rightarrow 15s\).
Μονάδες 7
Δ4) Να υπολογίσετε το έργο της \(\vec{F}\) στο χρονικό διάστημα \(10\rightarrow 15s\).
Μονάδες 6
Απάντηση Θέματος:
Ενδεικτική λύση
Δ1) Στο χρονικό διάστημα \(0 - 5 s\) η δύναμη είναι σταθερή, επομένως, σύμφωνα με τον 2ο νόμο του Νεύτωνα \(F = m\cdot α\) και η επιτάχυνση \(α\) θα είναι σταθερή.
Η κίνηση είναι ευθύγραμμη ομαλά επιταχυνόμενη.
Η επιτάχυνση θα έχει μέτρο:
$$α =\dfrac{Δυ}{Δt}= 2\dfrac{m}{s^2}$$
Δ2) Από τον 2ο νόμο του Νεύτωνα:
$$m =\dfrac{F}{α}= 4 kg$$
Δ3) \(0-5 s\): Κίνηση ευθύγραμμη ομαλά επιταχυνόμενη.
Όταν \(t = 5 s\) η ταχύτητα είναι:
$$υ_1 = 14\dfrac{m}{s}$$
\(5-10 s\) : Ευθύγραμμη ομαλή κίνηση με:
$$υ_2 = υ_1 = 14\dfrac{m}{s}$$
\(10-15 s\): Κίνηση ευθύγραμμη ομαλά επιβραδυνόμενη με:
$$|α'|=\dfrac{|F|}{m} = 1\dfrac{m}{s^2}$$
Όταν \(t = 15 s\) η ταχύτητα είναι:
$$υ_3 = υ_2 -|α'|Δt = 9\dfrac{m}{s}$$
Δ4) Στο χρονικό διάστημα \(10-15s\) η μετατόπιση υπολογίζεται από το εμβαδό του αντίστοιχου τραπεζίου:
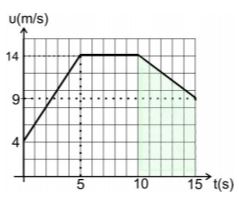
$$Δx=\dfrac{(14+9)}{2}\cdot 5m$$ $$\Rightarrow Δx=57,5m$$
Το έργο είναι:
$$W = F\cdot Δx = -230 J$$
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).