Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Α' Λυκείου |
|---|---|---|---|
| Μάθημα: | Φυσική | Θέμα: | 2 |
| Κωδικός Θέματος: | 13348 | Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 1.1.6. Η έννοια της μέσης ταχύτητας 1.1.7 Η έννοια της στιγμιαίας ταχύτητας 2.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ 2.1.1 Η έννοια του έργου |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Α' Λυκείου |
| Μάθημα: | Φυσική |
| Θέμα: | 2 |
| Κωδικός Θέματος: | 13348 |
| Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 1.1.6. Η έννοια της μέσης ταχύτητας 1.1.7 Η έννοια της στιγμιαίας ταχύτητας 2.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ 2.1.1 Η έννοια του έργου |
| Τελευταία Ενημέρωση: 29-Απρ-2023 | |
ΘΕΜΑ Β
Β1. Μαθητές μελετούν στο εργαστήριο ευθύγραμμες κινήσεις. Χρησιμοποιούν ένα μικρό αμαξίδιο, το οποίο με νήμα συνδέεται μέσω μιας μικρής τροχαλίας με ένα βαρίδι. Άφησαν το βαρίδι ελεύθερο και καθώς πέφτει προκαλεί μια επιταχυνόμενη κίνηση στο αμαξίδιο. Η κίνηση είναι ευθύγραμμη και το αμαξίδιο σέρνει πίσω του χαρτοταινία, στην οποία κατάλληλος μηχανισμός αφήνει στίγματα κάθε \(0,2\ s\).
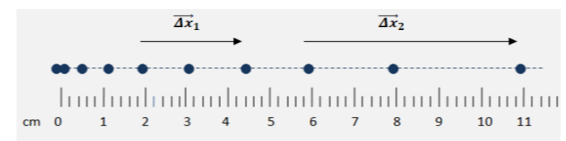
Οι μαθητές πήραν την χαρτοταινία και με τη βοήθεια υποδεκάμετρου σημείωσαν την τροχιά του κινητού, ενώνοντας με διακεκομμένη γραμμή τα στίγματα (κουκίδες), ενώ κάτω από αυτές σημείωσαν τις ενδείξεις του υποδεκάμετρου σε cm, αρχίζοντας με μηδέν στην πρώτη κουκίδα.
Ο καθηγητής τους υπέδειξε ότι η μέση ταχύτητα του κινητού για μετατόπιση μεταξύ τριών διαδοχικών κουκίδων, μπορεί να θεωρηθεί ως η στιγμιαία ταχύτητά του τη στιγμή που βρισκόταν στην μεσαία κουκίδα.
Με βάση την παραπάνω υπόδειξη, αν \(𝜐_1\) το μέτρο της στιγμιαίας ταχύτητας στη θέση που αντιστοιχεί στην κουκίδα \(𝑥_1=3 cm\) και \(𝜐_2\) το μέτρο της στιγμιαίας ταχύτητας στη θέση που αντιστοιχεί στην κουκίδα \(𝑥_2=8 cm\) του υποδεκάμετρου, ποια από τις παρακάτω σχέσεις, αποδίδει τον λόγο των μέτρων των δύο αυτών ταχυτήτων;
Α) Να επιλέξετε τη σωστή σχέση
α) \(\dfrac{𝜐_1}{𝜐_2}=1\)
β) \(\dfrac{𝜐_1}{𝜐_2}=0,48\)
γ) \(\dfrac{𝜐_1}{𝜐_2}=0,2\)
Μονάδες 4
B) Να αιτιολογήσετε την επιλογή σας.
Μονάδες 8
Β2. Από το μπαλκόνι του δευτέρου ορόφου ενός κτιρίου, με τη βοήθεια κάποιου μηχανισμού, εκτοξεύεται κατακόρυφα προς τα πάνω μια μικρή μπαλίτσα.
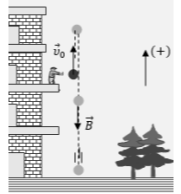
Η μπαλίτσα κινείται ελεύθερα ανεβαίνοντας μέχρι να μηδενιστεί η ταχύτητά της και αμέσως μετά επιστρέφει κινούμενη κατακόρυφα προς το έδαφος, όπως στο σχήμα. Η εκτόξευση της μπαλίτσας γίνεται τη χρονική στιγμή \(𝑡_0=0\) , η αρχική της ταχύτητα έχει μέτρο \(𝜐_0=20\ 𝑚/𝑠\) και το βάρος της \(𝐵=2\ N\).
Με θετική την προς τα πάνω φορά, η παρακάτω γραφική παράσταση αποδίδει τις τιμές ταχύτητας της μπαλίτσας, σε συνάρτηση με το χρόνο, από τη στιγμή της εκτόξευσής της, μέχρι να κτυπήσει στο έδαφος.
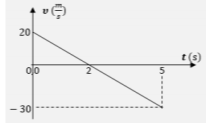
Το έργο του βάρους της μπαλίτσας από τη στιγμή της εκτόξευσής της, μέχρι να καταλήξει στο έδαφος είναι:
Α) Να επιλέξετε τη σωστή απάντηση:
α) \(𝑊_𝐵=50\ J\)
β) \(𝑊_𝐵=−50\ J\)
γ) \(𝑊_𝐵=130\ J\)
Μονάδες 4
Β) Να αιτιολογήσετε την επιλογή σας.
Μονάδες 9
Απάντηση Θέματος:
ΘΕΜΑ Β
Ενδεικτικές απαντήσεις
Β1.
Α) Σωστή η απάντηση β)
B) Αιτιολόγηση
Η κουκίδα στη θέση \(𝑥_1=3\ cm\) , είναι η έκτη κουκίδα. Θα βρούμε τη στιγμιαία ταχύτητα του σώματος στη θέση αυτή, ως μέση ταχύτητα αυτού κατά την μετατόπισή του από την πέμπτη, μέχρι την έβδομη κουκίδα. Κατά προσέγγιση παρατηρώντας την χαρτοταινία, αυτή η μετατόπιση φαίνεται να είναι από \(2\ cm\), μέχρι \(4,4\ cm\).
Ο χρόνος για την μετατόπιση αυτή είναι ο χρόνος για να καταγραφούν δύο κουκίδες από τον μηχανισμό, δηλαδή \(0,4\ s\).
Οπότε
\begin{align} 𝜐_1 & =\bar{υ} \\ & =\dfrac{𝛥𝑥_1}{𝛥𝑡} \\ & =\dfrac{(4,4−2)\ cm}{0,4\ s} \\ & =\dfrac{2,4\ cm}{0,4\ s} \\ & = 6 \dfrac{cm}{s}\ \ \ \ (1)\end{align}
Η κουκίδα στη θέση \(𝑥_2=8\ cm\) , είναι η ένατη κουκίδα. Θα βρούμε τη στιγμιαία ταχύτητα του σώματος στη θέση αυτή, ως μέση ταχύτητα αυτού κατά την μετατόπισή του από την όγδοη, μέχρι την δέκατη κουκίδα. Κατά προσέγγιση παρατηρώντας την χαρτοταινία, αυτή η μετατόπιση φαίνεται να είναι από \(6\ cm\), μέχρι \(11\ cm\).
Ο χρόνος για την μετατόπιση αυτή είναι ίδιος, δηλαδή \(0,4\ s\).
Οπότε
\begin{align} 𝜐_2 & =\bar{υ} \\ & =\dfrac{𝛥𝑥_2}{𝛥𝑡} \\ & =\dfrac{(11−6)\ cm}{0,4\ s} \\ & =\dfrac{5\ cm}{0,4\ s} \\ & = \dfrac{50}{4}\ \dfrac{cm}{s} \\ & = 12,5\ \dfrac{cm}{s}\ \ \ \ (2)\end{align}
Διαιρώντας κατά μέλη τις εξισώσεις \((1)\) και \((2)\):
$$\dfrac{𝜐_1}{𝜐_2}=\dfrac{6}{12,5}=\dfrac{24}{50}=\dfrac{48}{100}=0,48$$
B2.
A) Σωστή απάντηση η α)
B) Αιτιολόγηση
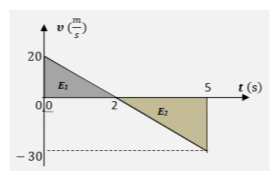
Με θετική την προς τα πάνω φορά, θα υπολογίσουμε την αλγεβρική τιμή της μετατόπισης της μπαλίτσας, από την στιγμή της εκτόξευσης μέχρι την πτώση της στο έδαφος, ως αλγεβρικό άθροισμα εμβαδών στο διάγραμμα ταχύτητας-χρόνου, των τριγώνων που δημιουργούνται από την γραφική παράσταση και των άξονα χρόνου.
\begin{align} 𝛥𝑥 & =𝐸_1−𝐸_2 \\ & =\dfrac{20\cdot 2}{2}\ m−\dfrac{30\cdot 3}{2}\ m \\ & =−25\ m \end{align}
Δηλαδή η μετατόπιση της μπαλίτσας έχει κατεύθυνση κατακόρυφη και προς τα κάτω, όπως και το βάρος της. Για το έργο του βάρους της μπαλίτσας, στην συνολική αυτή μετατόπισή της:
$$𝑊_𝐵=𝐵\cdot |𝛥𝑥|=2\cdot 25 J=𝟓𝟎\ 𝐉$$
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).