Τράπεζα Θεμάτων

www.trapeza-thematon.gr

Τύπος Σχολείου:	Γενικό Λύκειο	Τάξη:	Α' Λυκείου
Μάθημα:	Άλγεβρα	Θέμα:	4
Κωδικός Θέματος:	13368	Ύλη:	2.1. Οι Πράξεις και οι Ιδιότητές τους 2.2. Διάταξη Πραγματικών Αριθμών 2.4. Ρίζες Πραγματικών Αριθμών 3.3. Εξισώσεις 2ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Άλγεβρα
Θέμα:	4
Κωδικός Θέματος:	13368
Ύλη:	2.1. Οι Πράξεις και οι Ιδιότητές τους 2.2. Διάταξη Πραγματικών Αριθμών 2.4. Ρίζες Πραγματικών Αριθμών 3.3. Εξισώσεις 2ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού
Τελευταία Ενημέρωση: 19-Μαΐ-2023

ΘΕΜΑ 4

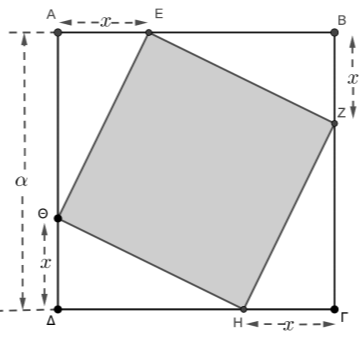
Στο παρακάτω σχήμα οι κορυφές του τετραγώνου $Ε Ζ Η Θ$ βρίσκονται πάνω στις πλευρές του τετραγώνου $Α Β Γ Δ$ .

α) Αν η πλευρά του τετραγώνου $Α Β Γ Δ$ είναι $α$ και η απόσταση των κορυφών του $Ε Ζ Η Θ$ από τις αντίστοιχες κορυφές του $Α Β Γ Δ$ είναι $x$ , όπως φαίνεται στο σχήμα, να δείξετε ότι το εμβαδόν του $Ε Ζ Η Θ$ δίνεται από τη σχέση:

$(Ε Ζ Η Θ) = x^{2} + (α - x)^{2} με 0 \leq x \leq α$

(Μονάδες 6)

β) Να δείξετε ότι το εμβαδόν του $Ε Ζ Η Θ$ δεν μπορεί να είναι μικρότερο από το μισό του εμβαδού $Α Β Γ Δ$ .
(Μονάδες 11)

γ) Να βρείτε την πλευρά $α$ του τετραγώνου $Α Β Γ Δ$ αν για $x = 1$ , το εμβαδόν του $Ε Ζ Η Θ$ είναι τα δύο τρίτα του εμβαδού του $Α Β Γ Δ$ , δηλαδή: $(Ε Ζ Η Θ) = \frac{2}{3} (Α Β Γ Δ)$ .
(Μονάδες 8)

(Δίνεται $\sqrt{3} \approx 1, 73$ )

Απάντηση Θέματος:

ΛΥΣΗ

α) Το εμβαδόν του $Ε Ζ Η Θ$ είναι $(Ε Ζ Η Θ) = (Θ Ε)^{2}$ . Στο ορθογώνιο τρίγωνο $Α Ε Θ$ είναι $(Α Ε) = x$ και $(Α Θ) = α - x$ . Από το πυθαγόρειο θεώρημα έχουμε:

$(Θ Ε)^{2} = (Α Ε)^{2} + (Α Θ)^{2}$

Άρα:

$(Ε Ζ Η Θ) = x^{2} + (α - x)^{2}$

Επίσης, επειδή το $Θ$ είναι σημείο της πλευράς $Δ Α$ και $x$ είναι η απόσταση από την κορυφή $Δ$ , θα είναι:

$0 \leq (Δ Θ) \leq (Δ Α)$ $\Leftrightarrow 0 \leq x \leq α$

β) Το εμβαδόν του $Α Β Γ Δ$ είναι $(Α Β Γ Δ) = α^{2}$ . Άρα η ζητούμενη σχέση γράφεται:

$(Ε Ζ Η Θ) \geq \frac{(Α Β Γ Δ)}{2}$ $\Leftrightarrow x^{2} + (a - x)^{2} \geq \frac{α^{2}}{2}$ $\Leftrightarrow 2 x^{2} + 2 (a - x)^{2} \geq α^{2}$ $\Leftrightarrow 2 x^{2} + 2 α^{2} - 4 α x + 2 x^{2} \geq α^{2}$ $\Leftrightarrow 4 x^{2} + α^{2} - 4 α x \geq 0$ $\Leftrightarrow (2 x)^{2} - 2 α 2 x + α^{2} \geq 0$ $\Leftrightarrow (2 x - α)^{2} \geq 0 που ισχύει$

γ) Από το ερώτημα α) για $x = 1$ είναι:

$(Ε Ζ Η Θ) = 1^{2} + (α - 1)^{2}$ $= 1 + α^{2} - 2 α + 1$ $= α^{2} - 2 α + 2$

Οπότε η σχέση $(Ε Ζ Η Θ) = \frac{2}{3} (Α Β Γ Δ)$ ισοδύναμα γίνεται:

$α^{2} - 2 α + 2 = \frac{2}{3} α^{2}$ $\Leftrightarrow 3 α^{2} - 6 α + 6 = 2 α^{2}$ $\Leftrightarrow α^{2} - 6 α + 6 = 0$

Η εξίσωση είναι δευτέρου βαθμού ως προς $α$ με διακρίνουσα $Δ = 6^{2} - 4 \cdot 6 = 12 > 0$ και ρίζες:

$α_{1,2} = \frac{6 \pm \sqrt{12}}{2}$ $= \frac{6 \pm 2 \sqrt{3}}{2}$ $= 3 \pm \sqrt{3}$ $\Leftrightarrow {\begin{cases} α_{1} = 3 - \sqrt{3} \approx 3 - 1, 73 = 1, 27 \\ α_{2} = 3 + \sqrt{3} \approx 4, 73 \end{cases}$

Από το ερώτημα α), πρέπει να ισχύει $x \leq α$ , η οποία για $x = 1$ γίνεται $1 \leq α$ .

Παρατηρούμε ότι και οι δύο τιμές είναι δεκτές.

Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).