Τράπεζα Θεμάτων

www.trapeza-thematon.gr

Τύπος Σχολείου:	Γενικό Λύκειο	Τάξη:	Β' Λυκείου
Μάθημα:	Γεωμετρία	Θέμα:	4
Κωδικός Θέματος:	14500	Ύλη:	9.2. Το Πυθαγόρειο θεώρημα

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Β' Λυκείου
Μάθημα:	Γεωμετρία
Θέμα:	4
Κωδικός Θέματος:	14500
Ύλη:	9.2. Το Πυθαγόρειο θεώρημα
Τελευταία Ενημέρωση: 15-Απρ-2024

ΘΕΜΑ 4

Δύο ίσοι κύκλοι $(K, R)$ και $(Λ, R)$ εφάπτονται εξωτερικά στο σημείο $Ο$ . Ένας τρίτος κύκλος $(Μ, ρ)$ εφάπτεται εξωτερικά με τους δύο κύκλους κέντρων $Κ$ και $Λ$ . Με κέντρο το σημείο $Ο$ και ακτίνα $2 R$ γράφουμε κύκλο, o οποίος εφάπτεται εξωτερικά των 3 παραπάνω κύκλων, όπως φαίνεται στο παρακάτω σχήμα.

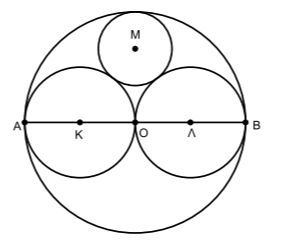
α) Στον παρακάτω πίνακα, στη στήλη $Α$ είναι οι διάκεντροι $K Λ$ , $Λ Μ$ και $Ο Μ$ των κύκλων με κέντρα $Κ$ , $Λ$ , $M$ και $Ο$ και στη στήλη $Β$ τα μήκη των διακέντρων αυτών. Να αντιστοιχίσετε τα στοιχεία της στήλης $Α$ με τα αντίστοιχα της στήλης $Β$ , γράφοντας στην κόλλα σας μόνο τις αντιστοιχίσεις.

Στήλη Α	Στήλη Β
Διάκεντρος	Μήκος
1. $Κ Λ$	i. $R$
2. $Λ Μ$	ii. $2 R$
3. $Ο Μ$	iii. $R + ρ$
	iv. $2 R - ρ$

(Μονάδες 06)

β)

Να αποδείξετε ότι το τρίγωνο $Μ Κ Λ$ είναι ισοσκελές και ότι το τμήμα $Μ Ο$ είναι το ύψος προς τη βάση του.
(Μονάδες 06)
Να βρείτε την ακτίνα $ρ$ του κύκλου κέντρου $M$ ως συνάρτηση του $R$ , όπου $R$ η ακτίνα των κύκλων κέντρων $Κ$ και $Λ$ .
(Μονάδες 13)

Απάντηση Θέματος:

ΛΥΣΗ

α) $1 \to i i$ , $2 \to i i i$ , $3 \to i v$ .
Δηλαδή $Κ Λ = 2 R$ γιατί οι κύκλοι κέντρων $K$ και $Λ$ εφάπτονται εξωτερικά, οπότε η διάκεντρός τους ισούται με το άθροισμα των ακτινών τους. Ομοίως $Λ Μ = R + ρ$ γιατί οι κύκλοι κέντρων $Λ$ και $M$ εφάπτονται εξωτερικά. Τέλος $Ο Μ = 2 R - ρ$ γιατί o κύκλος κέντρου $Ο$ με τον κύκλο κέντρου $M$ εφάπτονται εσωτερικά, οπότε η διάκεντρός τους θα ισούται με τη διαφορά των ακτινών τους.

β)

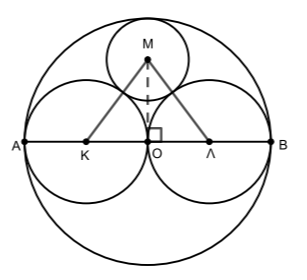
Οι κύκλοι $(K, R)$ και $(Μ, ρ)$ εφάπτονται εξωτερικά, οπότε η διάκεντρός τους θα ισούται με το άθροισμα των ακτινών τους, δηλαδή $K M = R + ρ = Λ Μ$ από το ερώτημα α). Άρα το τρίγωνο $Μ Κ Λ$ έχει δύο πλευρές ίσες, οπότε είναι ισοσκελές με βάση την πλευρά $Κ Λ$ . Το σημείο $Ο$ είναι το μέσο του τμήματος $Κ Λ$ γιατί $Ο Κ = Ο Λ = R$ επομένως το τμήμα $Μ Ο$ είναι διάμεσος της βάσης του ισοσκελούς τριγώνου, άρα είναι και ύψος, δηλαδή $Ο Μ ⊥ Κ Λ$ .
Στο ορθογώνιο τρίγωνο $Ο Μ Λ$ με $\hat{O} = 90^{0}$ εφαρμόζοντας το Πυθαγόρειο Θεώρημα έχουμε:
${Ο Μ}^{2} + {Ο Λ}^{2} = {Λ Μ}^{2}$
${(2 R - ρ)}^{2} + R^{2} = {(R + ρ)}^{2}$
$4 R^{2} - 4 R ρ + ρ^{2} + R^{2} = R^{2} + 2 R ρ + ρ^{2}$
$4 R^{2} = 6 R ρ$
$2 R = 3 ρ$
$ρ = \frac{2 R}{3}$ .

Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).