Τράπεζα Θεμάτων

ΘΕΜΑ 1

Α1. Στις τέσσερις πρώτες ερωτήσεις να γράψετε στην κόλλα σας το γράμμα Σ αν η πρόταση είναι σωστή ή το γράμμα Λ αν η πρόταση είναι λάθος, μετά από τον αριθμό της ερώτησης. Στην πέμπτη ερώτηση να γράψετε το γράμμα της σωστής απάντησης μετά από τον αριθμό της ερώτησης.

1. Αν \(α\le 0\) και \(ν\) άρτιος, τότε ισχύει \(\sqrt[ν]{α^{ν}}=|α|\).
2. Η γραφική παράσταση μιας συνάρτησης \(f(x)\) μπορεί να τέμνει τον άξονα \(y'y\) σε ακριβώς δύο σημεία.
3. Θεωρούμε την αριθμητική πρόοδο \((α_{ν})\) με πρώτο όρο \(α_{1}\) και διαφορά \(ω\). Το άθροισμα \(S_{ν}\) των \(ν\) πρώτων διαδοχικών όρων της \((α_{ν})\) δίνεται από την σχέση \(S_{ν}=\dfrac{ν}{2}[α_{1}+(ν-1)ω]\).
4. Η εξίσωση \(α\cdot x+β=0\) είναι αδύνατη ως προς \(x\), όταν \(α = 0\) και \(β \ne 0\).
5. 

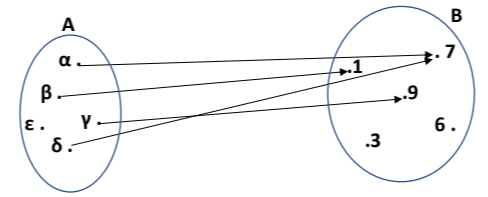
Στο παραπάνω σχήμα δίνεται μια αντιστοιχία στοιχείων ενός συνόλου \(Α\) σε στοιχεία ενός συνόλου \(Β\). Ποιο από τα παρακάτω είναι σωστό;
Α) η αντιστοιχία αυτή παριστάνει συνάρτηση από το σύνολο \(Α\) στο σύνολο \(Β\).
Β) η αντιστοιχία αυτή δεν παριστάνει συνάρτηση διότι στο \(3\) και στο \(6\) δεν αντιστοιχεί κανένα στοιχείο του \(Α\).
Γ) η αντιστοιχία αυτή δεν παριστάνει συνάρτηση διότι τα διαφορετικά στοιχεία \(α\) και \(δ\) του συνόλου \(Α\) αντιστοιχούν στο ίδιο στοιχείο του συνόλου \(Β\), το \(7\).
Δ) η αντιστοιχία αυτή δεν παριστάνει συνάρτηση διότι το στοιχείο \(ε\) δεν αντιστοιχεί σε κανένα στοιχείο του \(Β\).

(Μ10)

Α2. Έστω \(x_{1},x_{2}\) με \(x_{1}<x_{2}\) είναι οι δύο πραγματικές ρίζες του τριωνύμου \(f(x)=αx^{2}+ βx+γ\), \(x\in \mathbb{R}\). Να αποδείξετε ότι, αν για την μεταβλητή \(x\) ισχύει \(x<x_{1}\) ή \(x>x_{2}\) τότε τότε το τριώνυμο \(f(x)\) γίνεται ομόσημο του \(α\).

(Μ15)