Τράπεζα Θεμάτων

www.trapeza-thematon.gr

Τύπος Σχολείου:	Γενικό Λύκειο	Τάξη:	Β' Λυκείου
Μάθημα:	Άλγεβρα	Θέμα:	4
Κωδικός Θέματος:	15422	Ύλη:	3.1 Τριγωνομετρικοί Αριθμοί Γωνίας 3.2 Βασικές Τριγωνομετρικές Ταυτότητες 3.3 Αναγωγή στο 1o Τεταρτημόριο 3.4 Οι τριγωνομετρικές συναρτήσεις

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Β' Λυκείου
Μάθημα:	Άλγεβρα
Θέμα:	4
Κωδικός Θέματος:	15422
Ύλη:	3.1 Τριγωνομετρικοί Αριθμοί Γωνίας 3.2 Βασικές Τριγωνομετρικές Ταυτότητες 3.3 Αναγωγή στο 1o Τεταρτημόριο 3.4 Οι τριγωνομετρικές συναρτήσεις
Τελευταία Ενημέρωση: 10-Ιουν-2023

ΘΕΜΑ 4

Δίνεται η συνάρτηση $f (x) = a σ υ ν (\frac{π}{2} - 2 x) - 2 η μ (π + 2 x)$ με $a > 0$ , η οποία έχει μέγιστη τιμή το $4$ .

α) Να δείξετε ότι $f (x) = (a + 2) η μ 2 x$ .
(Μονάδες 5)

β)

Να δείξετε ότι $a = 2$ .
(Μονάδες 5)
Να βρείτε την περίοδο της $f$ .
(Μονάδες 5)

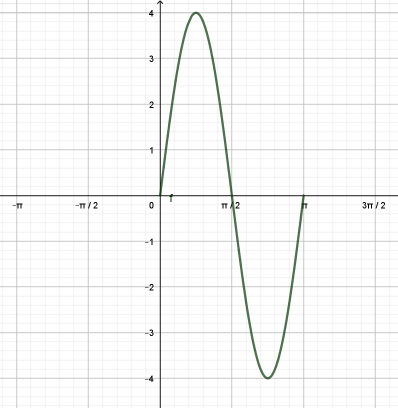
γ) Να παραστήσετε γραφικά τη συνάρτηση $f$ σε διάστημα μιας περιόδου.
(Μονάδες 5)

δ) Αν $g (x) = 5 - σ υ ν^{2} 2 x$ , να βρείτε, αν υπάρχουν, τα κοινά σημεία της $C_{f}$ με την $C_{g}$ , όπου $C_{f}, C_{g}$ οι γραφικές παραστάσεις των $f$ , $g$ αντίστοιχα.
(Μονάδες 5)

Απάντηση Θέματος:

ΛΥΣΗ

α) Είναι:

$f (x) = a σ υ ν (\frac{π}{2} - 2 x) - 2 η μ (π + 2 x)$ $= a η μ 2 x + 2 η μ 2 x$ $= (a + 2) η μ 2 x$

β)

Η μέγιστη τιμή της συνάρτησης $f$ καθορίζεται από το συντελεστή $a + 2$ . Πρέπει δηλαδή:

$a + 2 = 4$ $\Leftrightarrow α = 2$

Η περίοδος $Τ = \frac{2 π}{2} = π$ .

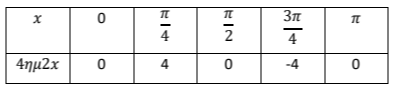
γ) Η γραφική παράσταση της $f (x) = 4 η μ 2 x$ στο διάστημα $[0, π]$ , βάσει του παρακάτω πίνακα:

δίνεται στο παρακάτω σχήμα:

δ) Για να βρούμε τις τετμημένες των κοινών σημείων των δύο γραφικών παραστάσεων λύνουμε την εξίσωση:

$f (x) = g (x)$ $\Leftrightarrow 4 η μ 2 x = 5 - σ υ ν^{2} 2 x$ $\Leftrightarrow 4 η μ 2 x = 5 - (1 - η μ^{2} 2 x)$ $\Leftrightarrow η μ^{2} 2 x - 4 η μ 2 x + 4 = 0$ $\Leftrightarrow (η μ 2 x - 2)^{2} = 0$ $\Leftrightarrow η μ 2 x = 2 αδύνατη$

Αφού η παραπάνω εξίσωση είναι αδύνατη, δεν υπάρχουν σημεία τομής των δύο γραφικών παραστάσεων.

Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).