Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Γ' Λυκείου |
|---|---|---|---|
| Μάθημα: | Μαθηματικά Προσανατολισμού | Θέμα: | 2 |
| Κωδικός Θέματος: | 23209 | Ύλη: | 1.3 Μονότονες συναρτήσεις - Αντίστροφη συνάρτηση |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Γ' Λυκείου |
| Μάθημα: | Μαθηματικά Προσανατολισμού |
| Θέμα: | 2 |
| Κωδικός Θέματος: | 23209 |
| Ύλη: | 1.3 Μονότονες συναρτήσεις - Αντίστροφη συνάρτηση |
| Τελευταία Ενημέρωση: 24-Οκτ-2022 | |
ΘΕΜΑ 2
Θεωρούμε τη συνάρτηση
α) Να αποδείξετε ότι η
(Μονάδες 9)
β) Να βρείτε το σύνολο τιμών της
(Μονάδες 8)
γ) Να αποδείξετε ότι υπάρχει η συνάρτηση
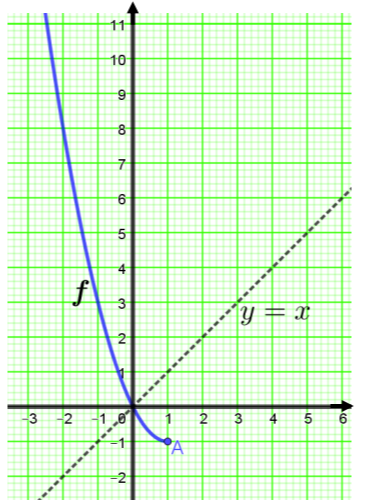
(Μονάδες 8)
Απάντηση Θέματος:
α) Έστω
για κάθε
Χρησιμοποιήσαμε τις ιδιότητες:
Εναλλακτικά, καθώς η
β) Επειδή η
γ) Αφού η συνάρτηση
Γνωρίζουμε ότι οι γραφικές παραστάσεις των συναρτήσεων
Επομένως, με προσεκτική χάραξη, παίρνουμε το παρακάτω σχήμα.
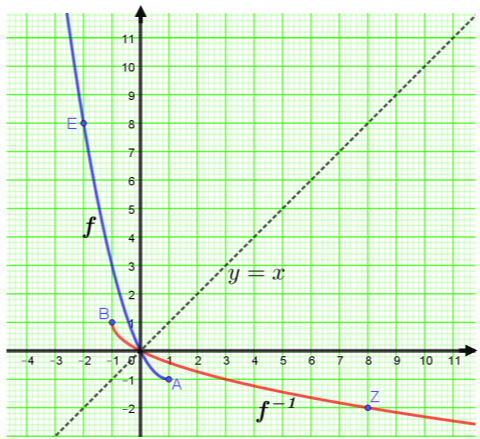
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).