Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Γ' Λυκείου |
|---|---|---|---|
| Μάθημα: | Μαθηματικά Προσανατολισμού | Θέμα: | 2 |
| Κωδικός Θέματος: | 26603 | Ύλη: | 1.2 Συναρτήσεις |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Γ' Λυκείου |
| Μάθημα: | Μαθηματικά Προσανατολισμού |
| Θέμα: | 2 |
| Κωδικός Θέματος: | 26603 |
| Ύλη: | 1.2 Συναρτήσεις |
| Τελευταία Ενημέρωση: 21-Φεβ-2023 | |
ΘΕΜΑ 2
Στο σχήμα δίνεται η γραφική παράσταση μιας συνάρτησης \(f\).
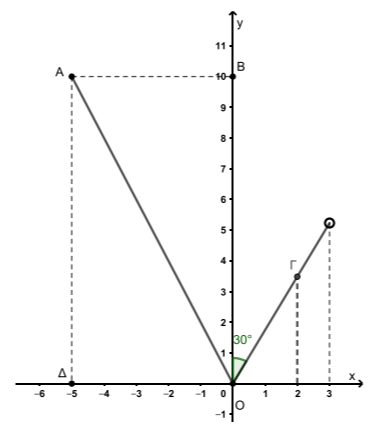
α) Nα βρείτε το πεδίο ορισμού και το σύνολο τιμών της συνάρτησης \(f\).
(Μονάδες 10)
β) Να προσδιορίσετε τον τύπο της συνάρτησης \(f\).
(Μονάδες 10)
γ) Ποιες είναι οι συντεταγμένες του σημείου \(Γ\);
(Μονάδες 5)
Απάντηση Θέματος:
ΛΥΣΗ

α) Το σύνολο των τετμημένων των σημείων της \(C_f\) αποτελεί το πεδίο ορισμού της συνάρτησης. Από τη γραφική παράσταση του σχήματος παρατηρούμε ότι το πεδίο ορισμού της συνάρτησης \(f\) είναι το διάστημα \([-5,3)\). Αντίστοιχα το σύνολο τιμών είναι το σύνολο των τεταγμένων των σημείων της \(C_f\), δηλαδή το κλειστό διάστημα \([0,10]\).
β) Για \(x \in [-5,0]\), η γραφική παράσταση της fαποτελεί τμήμα που βρίσκεται πάνω στην ευθεία που διέρχεται από την αρχή των αξόνων και από το σημείο \(Α(-5,10)\). Η ευθεία αυτή έχει εξίσωση της μορφής \(y=αx\) και επειδή διέρχεται από το σημείο \(Α(-5,10)\) θα ισχύει \(10= α(-5)\), οπότε \(α=-2\).
Για \(x \in (0,3)\), η γραφική παράσταση της \(f\) αποτελεί τμήμα που βρίσκεται πάνω στην ευθεία που διέρχεται από την αρχή των αξόνων και σχηματίζει με τον άξονα \(x’x\) γωνία \(60^0\). Η κλίση της ευθείας αυτής είναι ίση με \(εφ60^0= \sqrt{3}\), οπότε η εξίσωση της είναι η $y= \(\sqrt{3}x\).
Άρα: \(f(x) = \begin{cases} -2x\text{,}\ \ \ \text{όταν}\ \ x \in [-5,0] \\ \sqrt{3}x \text{,}\ \ \ \text{όταν}\ \ x \in (0,3) \end{cases}\)
γ) Η τετμημένη του σημείου \(Γ\) είναι \(2\). Για \(x=2\) στον τύπο της συνάρτησης \(y=\sqrt{3}x\) έχουμε, \(y= \sqrt{3} \cdot 2 = 2 \sqrt{3}\). Άρα \(Γ(2, 2\sqrt{3})\).
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).