Τράπεζα Θεμάτων

ΛΥΣΗ

α) Η συνάρτηση $f$ είναι συνεχής στο πεδίο ορισμού της, άρα και στο κλειστό διάστημα $[1,2]$ ως αθροίσματα γινομένων πολυωνυμικής με εκθετική και λογαριθμική.

• $f(1)=(1-2)e^1+(1-1)\ln 1=-e<0$
• $f(2)=(2-2)e^2+(2-1)\ln 2=\ln 2>0$ γιατί $1<2$, οπότε $\ln 1<\ln 2$, αφού η $\ln x$ είναι συνάρτηση γνησίως αύξουσα στο $(0,+\mathrm{\infty })$ και επειδή $\ln 1=0$, έχουμε ότι $\ln 2>0$.

Άρα $f(1)\cdot f(2)<0$, επομένως από Θεώρημα Bolzano η εξίσωση $f(x)=0$ έχει μία τουλάχιστον ρίζα $x_0\in (1,2)$, δηλαδή η γραφική παράσταση της $f$ τέμνει τον άξονα $x^{\prime }x$ σε ένα τουλάχιστον σημείο με τετμημένη $x_0\in (1,2)$.

β) Η συνάρτηση $f$ είναι παραγωγίσιμη στο πεδίο ορισμού της, ως αθροίσματα γινομένων πολυωνυμικής με εκθετική και λογαριθμική, με:

$$f^{\prime }(x)=e^x+(x-2)e^x+\ln x+{\displaystyle \frac{x-1}{x}}$$ $$=e^x(1+x-2)+\ln x+{\displaystyle \frac{x-1}{x}}$$ $$=e^x(x-1)+\ln x+{\displaystyle \frac{x-1}{x}}>=0$$ $$=(x-1)(e^x+{\displaystyle \frac{1}{x}})+\ln x$$

Για να υπάρχει μοναδικό σημείο της $C_f$ στο οποίο η εφαπτομένη ευθεία θα είναι οριζόντια, δηλαδή παράλληλη στον $x^{\prime }x$, θα πρέπει η εξίσωση $f^{\prime }(x)=0$ να έχει μοναδική ρίζα.

Παρατηρούμε ότι το $1$ είναι προφανής ρίζα της εξίσωσης $f^{\prime }(x)=0$, αφού:

$$f^{\prime }(1)=(1-1)(e+1)+\ln 1=0$$

• $f^{\prime }(x)>0$ γιατί για $x>1$ είναι $\ln x>0$ και $(x-1)(e^x+{\displaystyle \frac{1}{x}})>0$, αφού $(e^x+{\displaystyle \frac{1}{x}})>0$ για κάθε $x>0$ και
• $f^{\prime }(x)<0$ γιατί για $0<x<1$ είναι $\ln x<0$ και $(x-1)(e^x+{\displaystyle \frac{1}{x}})<0$

Κάνοντας τον πίνακα προσήμου της $f^{\prime }$ έχουμε:

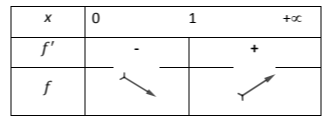
Άρα η $f$ είναι γνησίως φθίνουσα συνάρτηση στο $(0,1]$ και γνησίως αύξουσα στο $[1,+\mathrm{\infty })$.

Επομένως, αν ${\Delta }_1=(0,1]$, τότε $f({\Delta }_1)=[f(1),\underset{x\to 0}{lim}f(x))=[-e,+\mathrm{\infty })$

Γιατί:

$$\underset{x\to 0}{lim}f(x)=\underset{x\to 0}{lim}[(x-2)e^x+(x-1)\ln x]=+\mathrm{\infty }$$

Αφού:

$$\underset{x\to 0}{lim}(x-2)e^x=2e^0=-2$$

και:

$$\underset{x\to 0}{lim}(x-1)\ln x=-1(-\mathrm{\infty })=+\mathrm{\infty }$$

Αν ${\Delta }_2=[1,+\mathrm{\infty })$, τότε:

$$f({\Delta }_2)=[f(1),\underset{x\to +\mathrm{\infty }}{lim}f(x)]=[-e,+\mathrm{\infty })$$

Γιατί:

$$\underset{x\to +\mathrm{\infty }}{lim}f(x)=\underset{x\to +\mathrm{\infty }}{lim}[(x-2)e^x+(x-1)\ln x]=+\mathrm{\infty }$$

Αφού:

$$\underset{x\to +\mathrm{\infty }}{lim}(x-2)e^x=(+\mathrm{\infty })\cdot (+\mathrm{\infty })=+\mathrm{\infty }$$

και:

$$\underset{x\to +\mathrm{\infty }}{lim}(x-1)\cdot \ln x=(+\mathrm{\infty })\cdot (+\mathrm{\infty })=+\mathrm{\infty }$$

Το $0\in [-e,+\mathrm{\infty })=f({\Delta }_1)$, άρα υπάρχει ένα $x_1\in (0,1]$ τέτοιο ώστε $f(x_1)=0$, το οποίο είναι και μοναδικό γιατί η $f$ είναι γνησίως φθίνουσα στο $(0,1]$.

Το $0\in [-e,+\mathrm{\infty })=f({\Delta }_2)$, άρα υπάρχει ένα $x_2\in [1,+\mathrm{\infty })$ τέτοιο ώστε $f(x_2)=0$, το οποίο είναι επίσης μοναδικό γιατί η $f$ είναι γνησίως αύξουσα στο $[1,+\mathrm{\infty })$.

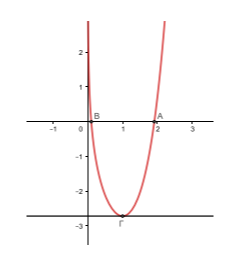
Επομένως, η γραφική παράσταση της $f$ τέμνει πράγματι τον άξονα $x^{\prime }x$ σε δύο ακριβώς σημεία τα $x_1$ και $x_2$ και το $x_2$ είναι το $x_0$ του α) ερωτήματος.