Τράπεζα Θεμάτων

www.trapeza-thematon.gr

Τύπος Σχολείου:	Γενικό Λύκειο	Τάξη:	Α' Λυκείου
Μάθημα:	Άλγεβρα	Θέμα:	4
Κωδικός Θέματος:	33587	Ύλη:	2.3. Απόλυτη Τιμή Πραγματικού Αριθμού 3.3. Εξισώσεις 2ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Άλγεβρα
Θέμα:	4
Κωδικός Θέματος:	33587
Ύλη:	2.3. Απόλυτη Τιμή Πραγματικού Αριθμού 3.3. Εξισώσεις 2ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού
Τελευταία Ενημέρωση: 21-Μαΐ-2023

ΘΕΜΑ 4

Δίνεται το τριώνυμο $f (x) = - x^{2} + 2 x + 3$ , $x \in R$ .

α) Να βρείτε το πρόσημο του παραπάνω τριωνύμου για τις διάφορες τιμές του $x \in R$ .
(Μονάδες 9)

β) Να βρείτε, αιτιολογώντας την απάντησή σας, το πρόσημο του γινομένου:

$f (2, 999) \cdot f (- 1, 002)$

(Μονάδες 7)

γ) Αν $- 3 < α < 3$ , να βρείτε το πρόσημο του αριθμού $- α^{2} + 2 | α | + 3$ .
(Μονάδες 9)

Απάντηση Θέματος:

ΛΥΣΗ

α) Το τριώνυμο $f (x) = - x^{2} + 2 x + 3$ έχει διακρίνουσα:

$Δ = 2^{2} - 4 \cdot (- 1) \cdot 3$ $= 4 + 12 = 16 > 0$

Το άθροισμα των ριζών του είναι:

$S = x_{1} + x_{2}$ $= \frac{- 2}{- 1} = 2$

και το γινόμενό τους είναι:

$P = x_{1} \cdot x_{2} = \frac{3}{- 1} = - 3$

Άρα $x_{1} = 3$ , $x_{2} = - 1$ και το πρόσημο του τριωνύμου είναι:

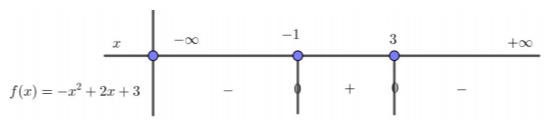
Οπότε το τριώνυμο παίρνει θετικές τιμές για $x \in (- 1, 3)$ και αρνητικές τιμές για $x \in (- \infty, - 1) \cup (3, + \infty)$ .

β) Εφόσον $2, 999 \in (- 1, 3)$ , από τον παραπάνω πίνακα προσήμου θα είναι $f (2, 999) > 0$ και επειδή $- 1, 002 < - 1$ θα είναι $f (- 1, 002) < 0$ . Άρα:

$f (2, 999) \cdot f (- 1, 002) < 0$

γ) Αν:

$- 3 < α < 3 \Leftrightarrow | α | < 3$

δηλαδή $0 \leq | α | < 3$ , τότε ο αριθμός $- α^{2} + 2 | α | + 3 = - | α |^{2} + 2 | α | + 3 = f (| α |)$ είναι θετικός, όπως προκύπτει από τον πίνακα προσήμου του τριωνύμου $f (x) = - x^{2} + 2 x + 3$ στο α) ερώτημα.

Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).