Τράπεζα Θεμάτων

ΑΠΑΝΤΗΣΗ ΘΕΜΑΤΟΣ 4ου
α) Για να κατασκευάσουμε τον πίνακα προσφοράς, πρέπει να γνωρίζουμε την παραγόμενη ποσότητα (Q), το μέσο μεταβλητό κόστος (AVC) και το οριακό κόστος (MC) σε όλους τους συνδυασμούς.
Γνωρίζουμε ότι: \(TC_{0}=FC \Rightarrow FC=4.000\ \text{€}\)

Υπολογίζουμε το μεταβλητό κόστος (VC) σε κάθε συνδυασμό:
Για \(Q_0 = 0\), \(VC_0 = 0\).

$$TC_{8}=FC+VC_{8} $$ $$\Leftrightarrow VC_{8}=TC_{8}-FC $$ $$\Leftrightarrow VC_{8}=4.800-4.000 $$ $$\Rightarrow VC_{8}=800\ \text{€}$$

$$TC_{20}=FC+VC_{20} $$ $$\Leftrightarrow VC_{20}=TC_{20}-FC $$ $$\Leftrightarrow VC_{20}=5.600-4.000 $$ $$\Rightarrow VC_{20}=1.600\ \text{€}$$

$$TC_{30}=FC+VC_{30} $$ $$\Leftrightarrow VC_{30}=TC_{30}-FC $$ $$\Leftrightarrow VC_{30}=6.400-4.000 $$ $$\Rightarrow VC_{30}=2.400\ \text{€}$$

$$TC_{38}=FC+VC_{38} $$ $$\Leftrightarrow VC_{38}=TC_{38}-FC $$ $$\Leftrightarrow VC_{38}=7.200-4.000 $$ $$\Rightarrow VC_{38}=3.200\ \text{€}$$

$$TC_{43}=FC+VC_{43} $$ $$\Leftrightarrow VC_{43}=TC_{43}-FC $$ $$\Leftrightarrow VC_{43}=8.000-4.000 $$ $$\Rightarrow VC_{43}=4.000 \ \text{€}$$

$$TC_{45}=FC+VC_{45} $$ $$\Leftrightarrow VC_{45}=TC_{45}-FC $$ $$\Leftrightarrow VC_{45}=8.800-4.000 $$ $$\Rightarrow VC_{45}=4.800\ \text{€}$$

Υπολογίζουμε το μέσο μεταβλητό κόστος (AVC) σε κάθε συνδυασμό:

$$AVC_{0}=\dfrac{VC_{0}}{Q_{0}}=- (\text{δεν ορίζεται})$$

$$AVC_{8}=\dfrac{VC_{8}}{Q_{8}}=\dfrac{800}{8}=100\ \text{€}$$

$$AVC_{20}=\dfrac{VC_{20}}{Q_{20}}=\dfrac{1.600}{20}=80\ \text{€}$$

$$AVC_{30}=\dfrac{VC_{30}}{Q_{30}}=\dfrac{2.400}{30}=80\ \text{€}$$

(σημείωση ΜΕΘΟΔΙΚΟΥ: Στην ενδεικτική λύση που δίνεται από το ΙΕΠ το \(AVC_{30}\) υπολογίζεται - λανθασμένα - ότι είναι 60 ευρώ. Ευχαριστούμε τον μαθητή που το επισήμανε)

$$AVC_{38}=\dfrac{VC_{38}}{Q_{38}}=\dfrac{3.200}{38}=84,2\ \text{€}$$

$$AVC_{43}=\dfrac{VC_{43}}{Q_{43}}=\dfrac{4.000}{43}=93\ \text{€}$$

$$AVC_{45}=\dfrac{VC_{45}}{Q_{45}}=\dfrac{4.800}{45}=106,6\ \text{€}$$

Υπολογίζουμε το οριακό (MC) σε κάθε συνδυασμό:

$$MC_{0}=\dfrac{Δ(VC)}{ΔQ}=- (\text{δεν ορίζεται})$$

$$MC_{8}=\dfrac{Δ(VC)}{ΔQ}=\dfrac{VC_{8}-VC_{0}}{Q_{8}-Q_{0}}=\dfrac{800-0}{8-0}=100\ \text{€}$$

$$MC_{20}=\dfrac{Δ(VC)}{ΔQ}=\dfrac{VC_{20}-VC_{8}}{Q_{20}-Q_{8}}=\dfrac{1.600-800}{20-8}=66,6\ \text{€}$$

$$MC_{30}=\dfrac{Δ(VC)}{ΔQ}=\dfrac{VC_{30}-VC_{20}}{Q_{30}-Q_{20}}=\dfrac{2.400-1.600}{30-20}=80\ \text{€}$$

$$MC_{38}=\dfrac{Δ(VC)}{ΔQ}=\dfrac{VC_{38}-VC_{30}}{Q_{38}-Q_{30}}=\dfrac{3.200-2.400}{38-30}=100\ \text{€}$$

$$MC_{43}=\dfrac{Δ(VC)}{ΔQ}=\dfrac{VC_{43}-VC_{38}}{Q_{43}-Q_{38}}=\dfrac{4.000-3.200}{43-38}=160\ \text{€}$$

$$MC_{45}=\dfrac{Δ(VC)}{ΔQ}=\dfrac{VC_{45}-VC_{43}}{Q_{45}-Q_{43}}=\dfrac{4.800-4.000}{45-43}=400\ \text{€}$$

Ο πίνακας με τα κόστη είναι ο ακόλουθος:

Q	TC	FC	VC	AVC	MC
0	4.000	4.000	0	-	-
8	4.800	4.000	800	100	100
20	5.600	4.000	1.600	80	66,6
30	6.400	4.000	2.400	60	80
38	7.200	4.000	3.200	84,2	100
43	8.000	4.000	4.000	93	160
45	8.800	4.000	4.800	106,6	400

Η επιχείρηση θα πρέπει να βρει την ποσότητα για την οποία μεγιστοποιείται το κέρδος της. Αυτό συμβαίνει, όταν το οριακό κόστος είναι ίσο με την τιμή (\(MC=P\)).

Το ανερχόμενο τμήμα της καμπύλης του οριακού κόστους, που βρίσκεται πάνω από την καμπύλη του μέσου μεταβλητού κόστους, αποτελεί τη βραχυχρόνια καμπύλη προσφοράς της επιχείρησης. (\(MC_{\text{ΑΝΕΡΧΟΜΕΝΟ}} \ge AVC\))

Άρα ο πίνακας προσφοράς της μεμονωμένης επιχείρησης είναι ο παρακάτω:

Συνδυασμός	P	QS
A	80	30
B	100	38
Γ	160	43
Δ	400	45

(Μονάδες 15)

β) Η καμπύλη προσφοράς είναι:

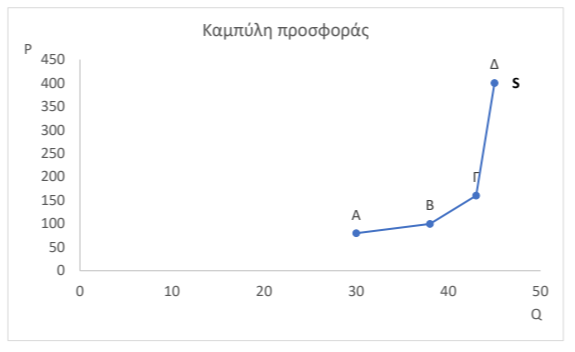
(Μονάδες 5)

γ) Ο πίνακας αγοραίας προσφοράς προκύπτει εάν σε κάθε τιμή αθροίσουμε τις ποσότητες που προσφέρουν όλες οι επιχειρήσεις που δραστηριοποιούνται στον κλάδο παραγωγής. Επειδή στον κλάδο υπάρχουν 50 ομοειδείς επιχειρήσεις, ο πίνακας αγοραίας προσφοράς θα είναι ο παρακάτω:

Συνδυασμός	P	\(Q_{S\ \text{ΑΓΟΡΑΙΑ}}\)
A	80	50 ∙ 30 = 1.500
B	100	50 ∙ 38 = 1.900
Γ	160	50 ∙ 43 = 2.150
Δ	400	50 ∙ 45 = 2.250

(Μονάδες 5)