Τράπεζα Θεμάτων

ΛΥΣΗ

α) Η γραφική παράσταση της \(f\) διέρχεται από το σημείο \(Α(0,2)\) για οποιαδήποτε τιμή του \(λ\), αν και μόνο αν ισχύει ότι \(f(0)=2\) για κάθε \(λ\in \mathbb{R}\).

Πράγματι είναι \(f(0)=(λ+1)\cdot 0^{2}-(λ+1)\cdot 0+2=2\) για κάθε \(λ\in \mathbb{R}\).

β) Για \(λ=-1\) ο τύπος της \(f\) γράφεται:

$$f(x)=(-1+1)x^{2}-(-1+1)x+2=2$$

Επομένως η γραφική παράσταση της \(f\) είναι μια ευθεία παράλληλη στον άξονα \(x'x\) που διέρχεται από το σημείο \(Α(0,2)\), όπως φαίνεται στο παρακάτω σχήμα.

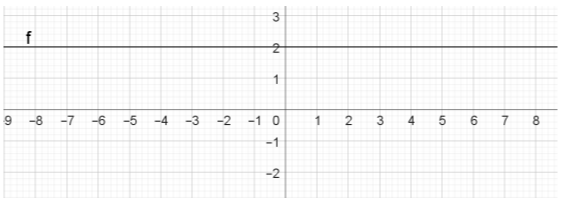
γ) Η γραφική παράσταση της \(f\) τέμνει τον άξονα \(x'x\) στο σημείο \(Β(2,0)\) και επομένως ισχύει ότι \(f(2)=0\). Είναι

$$f(2)=0 $$ $$\Leftrightarrow (λ+1)\cdot 2^{2}-(λ+1)\cdot 2+2=0 $$ $$\Leftrightarrow 4λ+4-2λ-2+2=0 $$ $$\Leftrightarrow 2λ=-4 $$ $$\Leftrightarrow λ=-2$$

Για \(λ=-2\) έχουμε:

$$f(x)=(-2+1)x^{2}-(-2+1)x+2$$ $$=-x^{2}+x+2$$

Οι τετμημένες των σημείων τομής της γραφικής παράστασης της \(f\) με τον \(x'x\) είναι οι λύσεις της εξίσωσης

$$f(x)=0 \Leftrightarrow -x^{2}+x+2=0$$

Το τριώνυμο \(-x^{2}+x+2\) έχει διακρίνουσα:

$$Δ=1^{2}-4\cdot (-1)\cdot 2$$ $$=1+8=9>0$$

και ρίζες τις:

$$x_{\text{1,2}}=\dfrac{-1\pm \sqrt{9}}{2\cdot (-1)}$$ $$=\dfrac{-1\pm 3}{-2} $$ $$\Rightarrow \begin{cases} x_{1} = \dfrac{-1+3}{-2} = \dfrac{2}{-2} = - 1 \\ \\ x_{2} = \dfrac{-1-3}{-2} = \dfrac{-4}{-2} =2 \end{cases}$$

Επομένως η γραφική παράσταση της \(f\) τέμνει τον \(x'x\) εκτός από το \(Β(2,0)\) και στο σημείο \((-1,0)\).

δ) Για \(λ=1\) ο τύπος της \(f\) γράφεται:

$$f(x)=(1+1)x^{2}-(1+1)x+2$$ $$=2x^{2}-2x+2$$ $$=2(x^{2}-x+1)$$

Το τριώνυμο \(x^{2}-x+1\) έχει διακρίνουσα:

$$Δ=(-1)^{2}-4\cdot 1\cdot 1$$ $$=1-4=-3 < 0$$

οπότε για κάθε \(x\in \mathbb{R}\) είναι ομόσημο του συντελεστή του \(x^{2}\), δηλαδή του \(α=1>0\).

Επομένως για κάθε \(x\in \mathbb{R}\) ισχύει ότι:

$$x^{2}-x+1>0 $$ $$\Leftrightarrow 2(x^{2}-x+1)>0 $$ $$\Leftrightarrow f(x)>0$$

που σημαίνει ότι η γραφική παράσταση της \(f\) βρίσκεται ολόκληρη πάνω από τον άξονα \(x'x\).