Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Α' Λυκείου |
|---|---|---|---|
| Μάθημα: | Φυσική | Θέμα: | 2 |
| Κωδικός Θέματος: | 7982 | Ύλη: | Χωρίς Αντιστοίχιση Ύλης |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Α' Λυκείου |
| Μάθημα: | Φυσική |
| Θέμα: | 2 |
| Κωδικός Θέματος: | 7982 |
| Ύλη: | Χωρίς Αντιστοίχιση Ύλης |
| Τελευταία Ενημέρωση: 25-Απρ-2024 | |
ΘΕΜΑ Β
Β1. Μικρή σφαίρα εκτοξεύεται από το έδαφος κατακόρυφα προς τα πάνω. Η επιτάχυνση της βαρύτητας \((g)\) είναι σταθερή και ως επίπεδο αναφοράς για τη βαρυτική δυναμική ενέργεια θεωρείται το έδαφος.
Α) Να επιλέξετε την σωστή πρόταση.
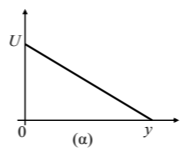
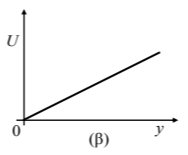
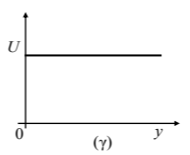
Η γραφική παράσταση της βαρυτικής δυναμικής ενέργειας \((U)\) της σφαίρας σε συνάρτηση με το ύψος \((y)\) από το σημείο εκτόξευσης έχει τη μορφή του διαγράμματος:
(α)
(β)
(γ)
Μονάδες 4
Β) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 8
Β2. Ένα κινητό εκτελεί ευθύγραμμη ομαλά επιταχυνόμενη κίνηση προς τη θετική φορά με επιτάχυνση ίση με \(α\) και τη χρονική στιγμή \(t = 0 s\) έχει ταχύτητα ίση με \(υ_0\). Μετά από χρόνο \(t\) έχει διανύσει διάστημα \(s\) και η ταχύτητά του είναι ίση με \(υ\).
Α) Να επιλέξετε την σωστή απάντηση.
Η ταχύτητα \(υ\) του κινητού μπορεί να υπολογιστεί από τη σχέση:
(α) \(υ^2=υ^2_0+2α\cdot s\)
(β) \(υ^2=υ^2_0+α\cdot s\)
(γ) \(υ^2=υ^2_0+4α\cdot s\)
Μονάδες 4
Β) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 9
Απάντηση Θέματος:
Β1. Σωστή η απάντηση (β)
Ενδεικτική Αιτιολόγηση
Η βαρυτική δυναμική ενέργεια δίδεται από τη σχέση \(U=m\cdot g\cdot y\), όπου \(m\) η μάζα της σφαίρας και \(y\) η απόσταση από το έδαφος.
Επομένως η ζητούμενη γραφική παράσταση είναι μια ευθεία που περνά από την αρχή των αξόνων.
Β2. Σωστή η απάντηση (α)
Ενδεικτική Αιτιολόγηση
α' τρόπος
Στην ευθύγραμμη ομαλά επιταχυνόμενη κίνηση οι εξισώσεις κίνησης είναι:
$$x=x_0+υ_0t+\dfrac{1}{2}αt^2, \ (1)$$
και
$$υ=υ_0+αt, \ (2)$$
Από την (1) έχουμε:
$$s= υ_0t+\dfrac{1}{2}αt^2, \ (3)$$
και
$$Δx=x-x_0 \text{ και } s=|Δx|$$
Aπαλείφοντας τον χρόνο στις σχέσεις (2) και (3) καταλήγουμε στη σχέση
$$υ^2=υ^2_0+2α\cdot s$$
β' τρόπος
Εφαρμόζοντας διαδοχικά το ΘΜΚΕ και τον 2ο Ν. Νεύτωνα έχουμε:
$$K_{τελ} -Κ_{αρχ}=W_{ΣF}$$ $$\dfrac{1}{2}mυ^{2}-\dfrac{1}{2}mυ^{2}_0=ΣF\cdot Δx$$ $$\dfrac{1}{2}mυ^2-\dfrac{1}{2}mυ^2_0=mα\cdot s$$
και τελικά:
$$υ^2=υ^2_0+2α\cdot s$$
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).