Τράπεζα Θεμάτων
www.trapeza-thematon.gr
| Τύπος Σχολείου: | Γενικό Λύκειο | Τάξη: | Α' Λυκείου |
|---|---|---|---|
| Μάθημα: | Φυσική | Θέμα: | 2 |
| Κωδικός Θέματος: | 8052 | Ύλη: | Χωρίς Αντιστοίχιση Ύλης |
| Τύπος Σχολείου: | Γενικό Λύκειο |
|---|---|
| Τάξη: | Α' Λυκείου |
| Μάθημα: | Φυσική |
| Θέμα: | 2 |
| Κωδικός Θέματος: | 8052 |
| Ύλη: | Χωρίς Αντιστοίχιση Ύλης |
| Τελευταία Ενημέρωση: 25-Απρ-2024 | |
ΘΕΜΑ Β
B1. Δύο μικρά σώματα Α, Β διαφορετικών μαζών, βρίσκονται πάνω σε λείο οριζόντιο δάπεδο. Το Α είναι ακίνητο ενώ το Β κινείται με σταθερή ταχύτητα μέτρου \(υ_1\) . Κάποια στιγμή ασκούμε την ίδια σταθερή οριζόντια δύναμη (προς την κατεύθυνση της ταχύτητας \(υ_1\)) για το ίδιο χρονικό διάστημα και στα δύο σώματα, με αποτέλεσμα αυτά να αποκτήσουν ταχύτητες ίδιου μέτρου.
Α) Να επιλέξετε την σωστή απάντηση:
Για τις μάζες των σωμάτων ισχύει:
α) \(m_A < m_B\)
β) \(m_A > m_B\)
γ) \(m_A = m_B\)
Μονάδες 4
Β) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 8
B2. Μαθητής της Α΄ Λυκείου παρατηρεί στο σχήμα τη γραφική παράσταση ταχύτητας - χρόνου ενός αυτοκινήτου, που κινείται σε ευθύγραμμο δρόμο.
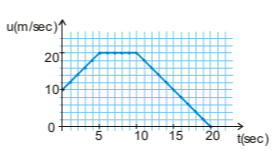
Ο μαθητής κάνει τον παρακάτω συλλογισμό, ερμηνεύοντας τη μορφή του διαγράμματος:
«Η επιταχυνόμενη κίνηση διαρκεί \(5 s\) (από \(0 s\) έως \(5 s\) ), ενώ η επιβραδυνόμενη διαρκεί \(10 s\) (από \(10 s\) έως \(20 s\)).
Αφού λοιπόν το χρονικό διάστημα που απαιτείται ώστε η ταχύτητα του αυτοκινήτου να μηδενιστεί είναι μεγαλύτερο από το χρονικό διάστημα που απαιτείται για να αυξηθεί η ταχύτητά του σε \(20 m/s\), συμπεραίνω ότι η επιτάχυνση έχει μεγαλύτερο μέτρο από την επιβράδυνση.»
Να επιβεβαιώσετε ή να διαψεύσετε τον παραπάνω συλλογισμό, δικαιολογώντας την απάντησή σας.
Μονάδες 13
Απάντηση Θέματος:
B1.
Α) Σωστή απάντηση είναι η α.
Β) Ενδεικτική αιτιολόγηση
Στα δύο σώματα ασκείται η ίδια δύναμη \(F\), για το ίδιο χρονικό διάστημα \(Δt\).
Για το σώμα Α, η μεταβολή της ταχύτητας είναι \(Δυ_Α = υ, \ (1)\)
Για το σώμα Β, η μεταβολή της ταχύτητας είναι \(Δυ_Β = υ - υ_1, \ (2)\)
Από τη σύγκριση των σχέσεων (1) και (2) προκύπτει: \(Δυ_Α > Δυ_Β\)
Για για το ίδιο χρονικό διάστημα \(Δt\) ισχύει:
$$\dfrac{Δυ_Α}{Δt}>\dfrac{Δυ_Β}{Δt}$$
Δηλαδή \(α_Α > α_Β\) και εφόσον \(ΣF_A = ΣF_B=ΣF\) συνεπάγεται [με χρήση του 2ου Νόμου του Νεύτωνα για κάθε σώμα] ότι:
$$\dfrac{ΣF}{m_A}>\dfrac{ΣF}{m_B}$$
Άρα: \(m_A < m_B\).
Συνεπώς σωστή είναι η πρόταση (α).
Β2.
Α) Ο παραπάνω συλλογισμός είναι Λάθος.
Β) Ενδεικτική αιτιολόγηση
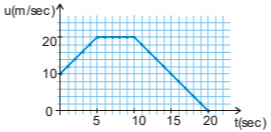
Από τη γραφική παράσταση, για \(t = 0 s\) μέχρι και \(t = 5 s\) παρατηρούμε ότι είναι: \(υ_{αρχ} = 0\dfrac{m}{s}\) και \(υ_{τελ} = 10\dfrac{m}{s}\). Οπότε ισχύει:
$$α_{0-5} =\dfrac{|Δυ|}{|Δt|}$$ $$\Rightarrow α_{0-5} =\dfrac {(10-0)m/s}{(5-0)s}$$ $$\Rightarrow α_{0-5} =\dfrac{10}{5}\dfrac{m}{s^2}=2\dfrac{m}{s^2}$$
Από τη γραφική παράσταση, για \(t = 10 s\) μέχρι και \(t = 20 s\) παρατηρούμε ότι η ταχύτητα είναι \(υ_{αρχ} = 10\dfrac{m}{s}\) και \(υ_{τελ} = 20\dfrac{m}{s}\). Οπότε είναι:
$$α_{10-20} =\dfrac{|Δυ|}{|Δt|}$$ $$\Rightarrow α_{10-20}=\dfrac{|(20-0)m/s}{(20-10)s}$$ $$\Rightarrow α_{10-20}=\dfrac{20}{10}\dfrac{m}{s^2}=2\dfrac{m}{s^2}$$
Παρατηρούμε ότι οι ισχύει:
$$|α_{0-5}| = |α_{10-20}|$$
Ο συλλογισμός του μαθητή είναι λάθος διότι πρέπει να υπολογίζουμε τη μεταβολή της ταχύτητας σε κάθε χρονικό διάστημα \(Δt.\)
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida).