Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
Έναρξη από 2 Σεπτεμβρίου
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 11938 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 12729 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 12-Μαρ-2024 | Ύλη: | 6.2. Γραφική Παράσταση Συνάρτησης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 12729 | ||
| Ύλη: | 6.2. Γραφική Παράσταση Συνάρτησης | ||
| Τελευταία Ενημέρωση: 12-Μαρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
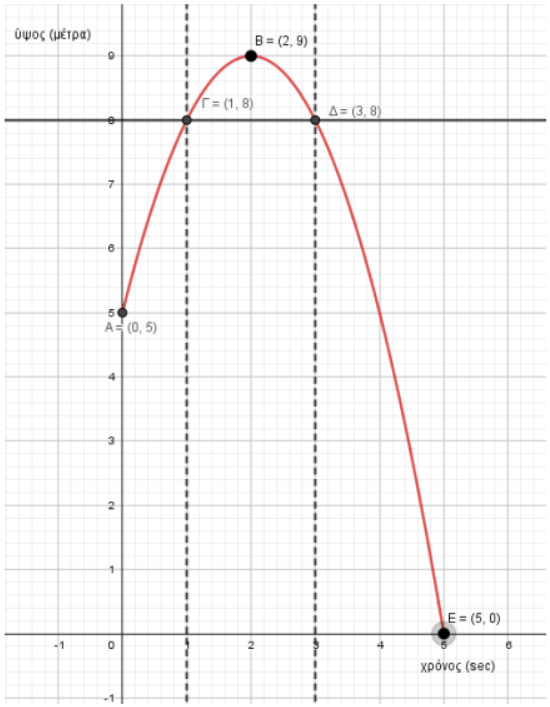
Ένα σώμα εκτελεί κατακόρυφη βολή, ώστε η απόστασή του από το έδαφος (μέτρα) σε σχέση με το χρόνο (sec) να φαίνονται στο παρακάτω διάγραμμα. Από τις πληροφορίες του διαγράμματος να απαντήσετε στις παρακάτω ερωτήσεις. Να δικαιολογήσετε τις απαντήσεις σας.
α. Από ποιο ύψος εκτελείται η κατακόρυφη βολή;
(Μονάδες 6)
β. Ποιο είναι το μέγιστο ύψος που φτάνει το σώμα και ποια χρονική στιγμή συμβαίνει αυτό;
(Μονάδες 6)
γ. Να βρείτε τις χρονικές στιγμές που το σώμα βρίσκεται σε ύψος \(8\) μέτρα από το έδαφος.
(Μονάδες 7)
δ. Να βρείτε τη χρονική στιγμή που το σώμα συναντά το έδαφος.
(Μονάδες 6)
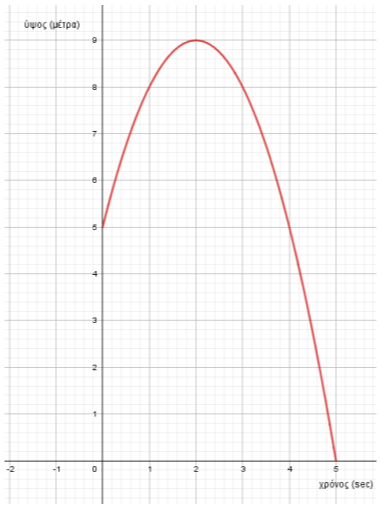
ΛΥΣΗ
α. Ως αρχή της μέτρησης έχουμε το σημείο \(Α(0,5)\). Οπότε για τη χρονική στιγμή \(t_1=0\ sec\) το σώμα βρίσκεται σε ύψος \(5\) μέτρα.
β. Το μέγιστο ύψος στο οποίο φτάνει το σώμα αντιστοιχεί στο σημείο \(Β(2,9)\). Οπότε τη χρονική στιγμή \(t_2=2\ sec\), το σώμα βρίσκεται στο μέγιστο ύψος που είναι \(9\) μέτρα.
γ. Αν φέρουμε την ευθεία \(y=8\), που αντιστοιχει σε ύψος \(8\) μέτρων, θα δούμε ότι τέμνει το διάγραμμα σε δύο σημεία. Αυτά είναι τα \(Γ(1,8)\) και \(Δ(3,8)\). Οπότε το σώμα βρίσκεται σε ύψος \(8\) μέτρα τις χρονικές στιγμές \(t_3=1\ sec\) και \(t_4=3\ sec\).
δ. Το έδαφος αντιστοιχεί στον άξονα \(x'x\) (ύψος = \(0\) μέτρα). Παρατηρούμε ότι το διάγραμμα έχει μόνο ένα κοινό σημείο με τον άξονα \(x'x\), το \(Ε\), που αντιστοιχεί και στο τέλος της μέτρησης. Οπότε το σώμα συναντά το έδαφος τη χρονική στιγμή \(t_5=5\ sec\).
