Θέμα: 15177

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 20153 φορές Επικοινωνία
Μάθημα:	Μαθηματικά Προσανατολισμού	Τάξη:	Β' Λυκείου
Κωδικός Θέματος:	15177	Θέμα:	4
Τελευταία Ενημέρωση:	23-Μαρ-2023	Ύλη:	1.4. Συντεταγμένες στο Επίπεδο 2.2. Γενική Μορφή Εξίσωσης Ευθείας 2.3. Εμβαδόν Τριγώνου 3.1 Ο Κύκλος
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Β' Λυκείου
Μάθημα:	Μαθηματικά Προσανατολισμού
Θέμα:	4
Κωδικός Θέματος:	15177
Ύλη:	1.4. Συντεταγμένες στο Επίπεδο 2.2. Γενική Μορφή Εξίσωσης Ευθείας 2.3. Εμβαδόν Τριγώνου 3.1 Ο Κύκλος
Τελευταία Ενημέρωση: 23-Μαρ-2023
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

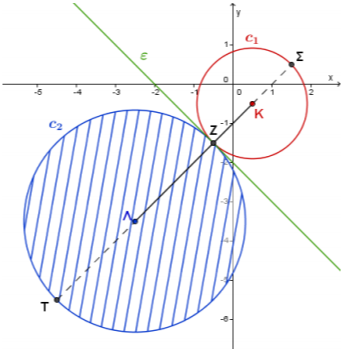
Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ 4

Δίνονται τα σημεία $A (1, 0)$ και $Β (0, - 1)$ , και ο κύκλος $c_{1}$ με εξίσωση

$c_{1} : {(x - \frac{1}{2})}^{2} + {(y + \frac{1}{2})}^{2} = 2.$

α) Να αποδείξετε ότι το σύνολο των σημείων $N (x, y)$ του επιπέδου τα οποία ικανοποιούν τη σχέση $\vec{N A^{2}} - \vec{N B^{2}} = 4$ ανήκουν στην ευθεία $(ε)$ με εξίσωση $y = - x - 2$ .
(Μονάδες 7)

β) Να αποδείξετε ότι το σύνολο των σημείων $P$ του επιπέδου τα οποία ικανοποιούν την εξίσωση

$2 x^{2} + 2 y^{2} + 10 x + 14 y + 21 = 0$

ανήκουν σε κύκλο $c_{2}$ κέντρου $Λ (- \frac{5}{2}, - \frac{7}{2})$ και ακτίνας $R = 2 \sqrt{2}$ .
(Μονάδες 6)

γ)

Να αποδείξετε ότι οι δύο κύκλοι, $c_{1}$ και $c_{2}$ , εφάπτονται εξωτερικά και στη συνέχεια να βρείτε την ελάχιστη και τη μέγιστη απόσταση των σημείων τους.
(Μονάδες 6)
Να αποδείξετε ότι η ευθεία $(ε)$ είναι η κοινή εφαπτομένη των κύκλων $c_{1}$ και $c_{2}$ .
(Μονάδες 6)

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

α) Θεωρούμε σημείο $N (x, y)$ του επιπέδου. Είναι $\vec{N A} = (1 - x, - y)$ και $\vec{N B} = (- x, - 1 - y)$ , οπότε ισχύει

$\begin{aligned} \vec{N A^{2}} - \vec{N B^{2}} = 4 \\ ⟺ & | \vec{N A} |^{2} - | \vec{N B} |^{2} = 4 \\ ⟺ & (1 - x)^{2} + y^{2} - x^{2} - (1 + y)^{2} = 4 \\ ⟺ & x + y + 2 = 0. \end{aligned}$

Άρα τα ζητούμενα σημεία $N$ ανήκουν σε ευθεία με εξίσωση $(ε) : y = - x - 2$ .

β) Έστω σημείο $P (x, y)$ του επιπέδου. Τότε, χρησιμοποιώντας τη μέθοδο συμπλήρωσης τετραγώνου, ισχύει

$\begin{aligned} 2 x^{2} + 2 y^{2} + 10 x + 14 y + 21 = 0 \\ ⟺ & x^{2} + y^{2} + 5 x + 7 y + \frac{21}{2} = 0 \\ ⟺ & x^{2} + 2 x \frac{5}{2} + {(\frac{5}{2})}^{2} + y^{2} + 2 y \frac{7}{2} + {(\frac{7}{2})}^{2} \\ = - \frac{21}{2} + \frac{25}{4} + \frac{49}{4} \\ ⟺ & c_{2} : {(x + \frac{5}{2})}^{2} + {(y + \frac{7}{2})}^{2} = 8. \end{aligned}$

Άρα τα σημεία $P$ ανήκουν πράγματι σε κύκλο $c_{2}$ με κέντρο $Λ (- \frac{5}{2}, - \frac{7}{2})$ και ακτίνα $R = 2 \sqrt{2}$ .

2ος τρόπος:
Έχουμε

$\begin{aligned} 2 x^{2} + 2 y^{2} + 10 x + 14 y + 21 = 0 \\ ⟺ & x^{2} + y^{2} + 5 x + 7 y + \frac{21}{2} = 0. \end{aligned}$

Αλλά:

$5^{2} + 7^{2} - 4 \cdot \frac{21}{2} = 32 > 0$

επομένως η εξίσωση παραστάνει πράγματι κύκλο, με κέντρο $Λ (- \frac{5}{2}, - \frac{7}{2})$ και ακτίνα $R = 2 \sqrt{2}$ .

γ)

Οι κύκλοι $c_{1}$ και $c_{2}$ εφάπτονται εξωτερικά, διότι έχουν διάκεντρο

$\begin{aligned} δ & = (Κ Λ) \\ = \sqrt{{(\frac{1}{2} + \frac{5}{2})}^{2} + {(\frac{- 1}{2} + \frac{7}{2})}^{2}} \\ = 3 \sqrt{2} \end{aligned}$

και ισχύει $δ = ρ + R$ .

Άρα η ελάχιστη απόσταση των σημείων των δύο κύκλων είναι μηδέν και η μέγιστη απόσταση είναι ίση με $Σ Τ = Σ Ζ + Ζ Τ = 2 ρ + 2 R = 6 \sqrt{2}$ .

Είναι

$d (K, ε) = \frac{| \frac{1}{2} - \frac{1}{2} + 2 |}{\sqrt{2}} = \sqrt{2} = ρ$

και

$d (Λ, ε) = \frac{| - \frac{5}{2} - \frac{7}{2} + 2 |}{\sqrt{2}} = 2 \sqrt{2} = R .$

Άρα η ευθεία $(ε)$ είναι η ζητούμενη κοινή εφαπτομένη.