Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 8972 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 23112 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 21-Μαρ-2023 | Ύλη: | 1.3 Απλή αρμονική ταλάντωση 4.8 Κίνηση φορτισμένων σωματιδίων μέσα σε μαγνητικό πεδίο (εκτός από «Δ. Κίνηση σε ανομοιογενές μαγνητικό πεδίο») | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 23112 | ||
| Ύλη: | 1.3 Απλή αρμονική ταλάντωση 4.8 Κίνηση φορτισμένων σωματιδίων μέσα σε μαγνητικό πεδίο (εκτός από «Δ. Κίνηση σε ανομοιογενές μαγνητικό πεδίο») | ||
| Τελευταία Ενημέρωση: 21-Μαρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
2.1. Σε εργαστήριο Φ.Ε. διαθέτουμε δύο ελατήρια σταθεράς \(k_{1}\) και \(k_{2}\) και ένα σώμα μάζας \(m\). Επίσης διαθέτουμε σειρά βαριδίων με μάζες των \(20\ g\), \(50\ g\), \(80\ g\) και \(0,1\ Κg\). Κρεμάμε το ελατήριο \(1\) σε βαθμολογημένο στάτορα έτσι ώστε ο αβαρής δίσκος που τοποθετείται στο κάτω άκρο του ελατηρίου να είναι στο σημείο μηδέν της κλίμακας. Κάποιος μαθητής τοποθετεί ποικιλία βαριδίων στο δίσκο του ελατηρίου \(1\) και συμπληρώνει τον παρακάτω πίνακα τιμών:
| Μάζα (g) | Απόσταση Δl (cm) Φ.Μ. – Θ.Ι. |
|---|---|
| 50 | 1 |
| 130 | 2,6 |
| 180 | 3,6 |
| 250 | 5 |
Άλλος μαθητής δουλεύοντας με το ελατήριο \(2\), παραδίδει το παρακάτω διάγραμμα:
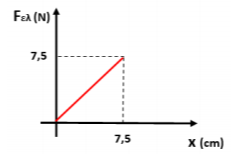
Τοποθετούμε διαδοχικά στο δίσκο των δύο ελατηρίων το σώμα μάζας \(m\) και θέτουμε σε ταλάντωση ίδιου πλάτους \(Α\) τους δύο ταλαντωτές. Για τις δύο ταλαντώσεις ισχύει:
(α) Η μέγιστη επιτάχυνση της ταλάντωσης \(1\) είναι μεγαλύτερη από την μέγιστη επιτάχυνση της ταλάντωσης \(2\) και ο λόγος τους είναι: \(\dfrac{α_{\text{max}_1}}{α_{\text{max}_2}}=\sqrt{2}\).
(β) Η μέγιστη επιτάχυνση της ταλάντωσης \(1\) είναι ίση με την μέγιστη επιτάχυνση της ταλάντωσης \(2\).
(γ) Η μέγιστη επιτάχυνση της ταλάντωσης \(2\) είναι μεγαλύτερη από την μέγιστη επιτάχυνση της ταλάντωσης \(1\) και ο λόγος τους είναι: \(\dfrac{α_{\text{max}_1}}{α_{\text{max}_2}}=\dfrac{1}{2}\).
2.1.Α. Να επιλέξετε την ορθή πρόταση.
Μονάδες 4
2.1. B. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 8
2.2. . Σε χώρο όπου συνυπάρχουν Ομογενές Ηλεκτρικό και Ομογενές Μαγνητικό Πεδίο, με τις δυναμικές τους γραμμές κάθετες μεταξύ τους, εισέρχεται σωμάτιο μάζας \(m=100\ g\) και φορτίου \(q=-20\ mC\), κινούμενο με ταχύτητα μέτρου \(υ_{0}=50\ \dfrac{m}{s}\) (βλ. σχήμα).
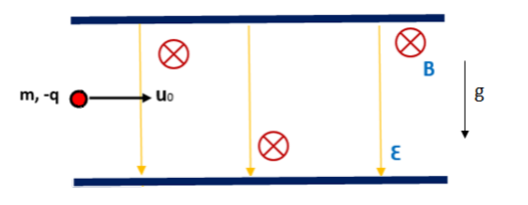
Η ταχύτητα σχηματίζει ορθές γωνίες με τις εντάσεις των πεδίων.
Δίνονται \(Ԑ=50\dfrac{Ν}{C}\), \(Β=2 T\) και \(g=10\ \dfrac{m}{s^{2}}\).
Για έναν εξωτερικό παρατηρητή η κίνηση του σωματίου είναι:
(α) ευθύγραμμη ομαλή,
(β) ομαλή κυκλική,
(γ) παραβολική με φορά προς τα κάτω.
2.2.Α. Να επιλέξετε την ορθή πρόταση.
Μονάδες 4
2.2.Β. Να αιτιολογήσετε την επιλογή σας.
Μονάδες 9
ΘΕΜΑ 2
2.1.
2.1. Α. Σωστή απάντηση η (γ)
Μονάδες 4
2.1.B.
Από το πείραμα που εκτέλεσε ο πρώτος μαθητής και τον πίνακα τιμών που μας παρείχε προκύπτει γραμμική μεταβολή της δύναμης του βάρους των βαριδίων που χρησιμοποίησε, ανάλογη με την απόσταση. Επειδή στη θέση ισορροπίας οι δυνάμεις των βαρών των βαριδίων και οι δυνάμεις επαναφοράς του ελατηρίου είναι αντίθετες σε κάθε μέτρηση, ο συντελεστής κλίσης της ευθείας είναι:
$$k_{1}=\dfrac{W_{1}}{x_{1}}$$ $$\Rightarrow k_1 =\dfrac{50\cdot 10^{-3}\ Kg\cdot 10\ m/s^{2}}{1\cdot 10^{-2}\ m}$$ $$\Rightarrow k_1 =50\ \dfrac{N}{m}$$
Από το διάγραμμα που μας παρείχε ο δεύτερος μαθητής, μπορούμε να υπολογίσουμε την σταθερά \(k_{2}\):
$$ k_{2}=\dfrac{F_{ελ}}{x} $$ $$\Rightarrow k_2=\dfrac{7,5\ N}{7,5\cdot 10^{-2}\ m}$$ $$\Rightarrow k_2=100\ \dfrac{N}{m}$$
Θέτοντας σε ταλάντωση τους δύο ταλαντωτές με την ίδια μάζα \(m\) και το ίδιο πλάτος \(Α\), οι μέγιστες επιταχύνσεις που προκύπτουν έχουν λόγο:
$$ \dfrac{α_{\text{max}_1}}{α_{\text{max}_2}}=\dfrac{ω_{1}^{2}Α}{ω_{2}^{2}Α}=\dfrac{\dfrac{k_{1}}{m}}{\dfrac{k_{2}}{m}}=\dfrac{k_{1}}{k_{2}}$$ $$\Rightarrow \dfrac{α_{\text{max}_1}}{α_{\text{max}_2}}=\dfrac{50\ \dfrac{N}{m}}{100\ \dfrac{N}{m}}=\dfrac{1}{2} $$
Άρα η μέγιστη επιτάχυνση του δεύτερου ταλαντωτή είναι μεγαλύτερη και ο λόγος τους είναι:
$$\dfrac{α_{\text{max}_1}}{α_{\text{max}_2}}=\dfrac{1}{2}$$
Μονάδες 8
2.2.
2.2.A. Σωστή απάντηση η (β)
Μονάδες 4
2.2.B.
Οι δυνάμεις που ασκούνται στο σωματίδιο, όπως φαίνονται στο σχήμα, είναι:
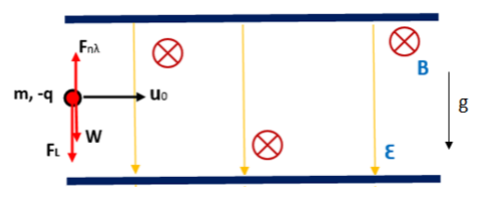
Για τα μέτρα τους ισχύει:
$$F_{\text{Lorentz}}=Buq=2T\cdot 50\ \dfrac{m}{s}\cdot 20\cdot 10^{-3}\ C $$ $$\Leftrightarrow F_{\text{Lorentz}}=2\ N$$ $$\Leftrightarrow F_{ηλ}=Ԑ|q|=50\ \dfrac{N}{C}\cdot 20\cdot 10^{-3}\ C $$ $$\Leftrightarrow F_{ηλ}=1\ N$$ $$\Leftrightarrow W=mg=0,1\ Kg\cdot 10\ \dfrac{m}{s^{2}} $$ $$\Leftrightarrow W=1\ N$$
Παρατηρούμε ότι το βάρος και η δύναμη από το ηλεκτρικό πεδίο είναι πάντοτε αντίθετες, άρα έχουν συνισταμένη μηδέν. Δηλαδή, η μόνη δύναμη που επιδρά στην κίνηση του σωματίου είναι η \(\vec{F}_{\text{Lorentz}}\), η οποία, κατά τα γνωστά, παίζει τον ρόλο κεντρομόλου δύναμης. Κατά συνέπεια, η κίνηση είναι ομαλή κυκλική.
Μονάδες 9