Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 11356 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 25610 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 06-Ιουν-2023 | Ύλη: | 4.2 Οι κινήσεις των στερεών σωμάτων 4.4 Ισορροπία στερεού σώματος | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 25610 | ||
| Ύλη: | 4.2 Οι κινήσεις των στερεών σωμάτων 4.4 Ισορροπία στερεού σώματος | ||
| Τελευταία Ενημέρωση: 06-Ιουν-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Στην περιφέρεια μιας ακίνητης τροχαλίας, ακτίνας
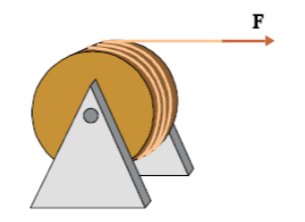
Βρέθηκε πως όταν η τροχαλία έχει κάνει
4.1. Το μέτρο της γωνιακής επιτάχυνσης της τροχαλίας.
Μονάδες 6
4.2. Τηγραμμική ταχύτητα του ανώτερου σημείου της τροχαλίας την χρονική στιγμή
Μονάδες 6
4. 3. Την συνολική ροπή των δυνάμεων που δέχεται η τροχαλία ως προς τον άξονα περιστροφής της.
Μονάδες 6
4. 4. Το μήκος του νήματος που ξετυλίγεται από την τροχαλία στην διάρκεια του τέταρτου δευτερολέπτου της κίνησής της.
Μονάδες 7
ΘΕΜΑ 4
4.1. Η τροχαλία, υπό την επίδραση της ροπής της δύναμης
Η γραφική παράσταση γωνιακής ταχύτητας-χρόνου είναι η επόμενη:
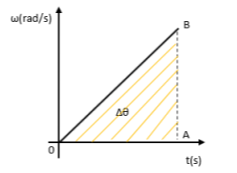
Το εμβαδό του γραμμοσκιασμένου τριγώνου είναι αριθμητικά ίσο με την επίκεντρη γωνία που διαγράφει οποιαδήποτε επιβατική ακτίνα της τροχαλίας. Άρα,
Όταν η τροχαλία έχει διαγράψει
Θα κάνουμε απαλοιφή του χρόνου από τις σχέσεις
Μονάδες 6
4.2. Την χρονική στιγμή
Ηγραμμική ταχύτητα στο ανώτερο σημείο της τροχαλίας έχει την ίδια διεύθυνση με το νήμα, φορά προς τα δεξιά και μέτρο:
Μονάδες 6
4. 3. Η τροχαλία δέχεται τρεις δυνάμεις, το βάρος της
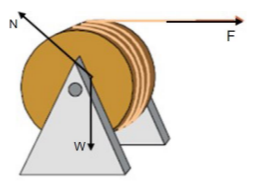
Ορίζοντας ως θετική φορά την φορά περιστροφής της τροχαλίας, η συνολική ροπή ως προς τον άξονα είναι:
Μονάδες 6
4. 4. Η επίκεντρη γωνία που διαγράφει η επιβατική ακτίνα κάθε σημείου της τροχαλίας από την χρονική στιγμή
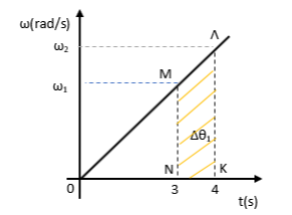
Το μήκος του νήματος που ξετυλίγεται είναι ίσο με το μήκος τόξου της περιφέρειας της τροχαλίας που αντιστοιχεί σε επίκεντρη γωνία
Μονάδες 7