Θέμα: 8004

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 6182 φορές Επικοινωνία
Μάθημα:	Φυσική	Τάξη:	Α' Λυκείου
Κωδικός Θέματος:	8004	Θέμα:	2
Τελευταία Ενημέρωση:	24-Οκτ-2024	Ύλη:	Χωρίς Αντιστοίχιση Ύλης
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Φυσική
Θέμα:	2
Κωδικός Θέματος:	8004
Ύλη:	Χωρίς Αντιστοίχιση Ύλης
Τελευταία Ενημέρωση: 24-Οκτ-2024
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ Β

Β1. Ένας αστροναύτης επιχειρεί να μετρήσει την επιτάχυνση της βαρύτητας κοντά στην επιφάνεια ενός πλανήτη που δεν έχει ατμόσφαιρα. Για το σκοπό αυτό αφήνει να πέσει μια μικρή σφαίρα από ύψος $1, 5 m$ οπότε διαπιστώνει ότι η σφαίρα φτάνει στην επιφάνεια μετά από χρόνο $3 s$ .

Α) Να επιλέξετε την σωστή απάντηση
Ο αστροναύτης συμπεραίνει ότι το μέτρο της επιτάχυνσης της βαρύτητας είναι ίσο με:
α) $1 m / s^{2}$
β) $\frac{1}{2} m / s^{2}$
γ) $\frac{1}{3} m / s^{2}$
Μονάδες 4

B) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 8

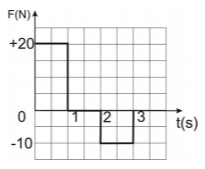
Β2. Κιβώτιο βρίσκεται ακίνητο σε λείο οριζόντιο επίπεδο. Τη χρονική στιγμή $t = 0 s$ στο κιβώτιο ασκείται οριζόντια δύναμη σταθερής διεύθυνσης η τιμή της οποίας σε συνάρτηση με το χρόνο δίνεται από το διάγραμμα που παριστάνεται στην παρακάτω εικόνα, οπότε το κιβώτιο αρχίζει να κινείται κατά τη θετική φορά του άξονα $x$ .

Α) Να επιλέξετε την σωστή απάντηση
Τη χρονική στιγμή $t = 3 s$ , το κιβώτιο:
α) εξακολουθεί να κινείται κατά τη θετική φορά του άξονα $x$ .
β) ηρεμεί.
γ) κινείται κατά την αρνητική φορά του άξονα $x$ .
Μονάδες 4

B) Να δικαιολογήσετε την επιλογή σας.
Μονάδες 9

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

B1.
A) Σωστή απάντηση είναι η (γ)

B) Ενδεικτική Αιτιολόγηση
Η σφαίρα εκτελεί ελεύθερη πτώση, άρα το ύψος και ο χρόνος πτώσης συνδέονται με τη σχέση:

$h = \frac{1}{2} \cdot g^{'} \cdot t^{2}$

όπου $g^{'}$ η επιτάχυνση της βαρύτητας κοντά στην επιφάνεια του πλανήτη.
Από αυτήν προκύπτει ότι

$g^{'} = \frac{2 h}{t^{2}} = \frac{1}{3} m / s^{2}$

B2.
A) Σωστή απάντηση είναι η (α)

B) Ενδεικτική Αιτιολόγηση
Χρονικό διάστημα $0 - t_{1}$ : Κίνηση ευθύγραμμη ομαλά επιταχυνόμενη με

$α = \frac{F}{m} και υ = α \cdot t = (\frac{F}{m}) \cdot t_{1} > 0$

Χρονικό διάστημα $t_{1} - t_{2}$ : Κίνηση ευθύγραμμη ομαλή με $υ = (\frac{F}{m}) \cdot t_{1}$

Χρονικό διάστημα $t_{2} - t_{3}$ : Κίνηση ευθύγραμμη ομαλά επιβραδυνόμενη με $α^{'} = \frac{F^{'}}{m}$ .

Επειδή:

$F^{'} = \frac{F}{2} θα είναι α^{'} = \frac{F}{2 m}$

Η ταχύτητα σε αυτό το χρονικό διάστημα θα είναι:

$υ^{'} = υ - α^{'} t ή υ^{'} = (\frac{F}{m}) \cdot t_{1} - \frac{F^{'}}{m} (t_{3} - t_{2})$ $υ^{'} = (\frac{F}{m}) \cdot t_{1} - (\frac{F}{2 m}) \cdot (t_{3} - t_{2})$

Αλλά $t_{1} = t_{3} - t_{2} = 1 s .$

Άρα $υ^{'} = (\frac{F}{2 m}) \cdot t_{1} > 0.$