Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 12057 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 13346 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 21-Φεβ-2024 | Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 1.3 ΔΥΝΑΜΙΚΗ ΣΤΟ ΕΠΙΠΕΔΟ 1.3.4 Ανάλυση δύναμης σε συνιστώσες 1.3.6 Ισορροπία ομοεπιπέδων δυνάμεων | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 13346 | ||
| Ύλη: | 1.1 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ 1.3 ΔΥΝΑΜΙΚΗ ΣΤΟ ΕΠΙΠΕΔΟ 1.3.4 Ανάλυση δύναμης σε συνιστώσες 1.3.6 Ισορροπία ομοεπιπέδων δυνάμεων | ||
| Τελευταία Ενημέρωση: 21-Φεβ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ Β
Β1. Ένα σημειακό αντικείμενο κινείται ευθύγραμμα. Ορίσαμε άξονα
Ως προς το σύστημα αναφοράς που δημιουργήσαμε, δίνεται ο παρακάτω πίνακας, σε κάθε οριζόντια γραμμή του οποίου καταγράφονται: η θέση
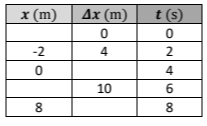
A) Να συμπληρώσετε τις τιμές που λείπουν.
Μονάδες 4
Β) Να αιτιολογήσετε τις επιλογές σας.
Μονάδες 8
B2. Ένα ιστιοφόρο πλέει με σταθερή ταχύτητα και κατεύθυνση προς τον Βορρά.

Η κατεύθυνση πλεύσης καθορίζεται από την πλάγια δύναμη
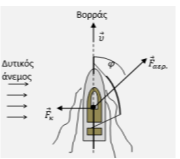
Η δύναμη
Για τη γωνία δίνεται
Α) Το μέτρο της δύναμης
α)
β)
γ)
(Να επιλέξετε τη σωστή απάντηση)
Μονάδες 4
Β) Αιτιολογήστε την επιλογή σας.
Μονάδες 9
ΘΕΜΑ Β
Ενδεικτικές απαντήσεις
Β1.
Α) Δίνεται παρακάτω ο πίνακας με συμπληρωμένες τις τιμές που έλειπαν από τον αρχικό.
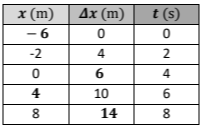
Β) Αιτιολόγηση:
Έστω
Αν
- Εφαρμόζουμε την
- Εφαρμόζουμε την
- Εφαρμόζουμε την
- Εφαρμόζουμε την
B2.
A) Σωστή η απάντηση β)
B) Αιτιολόγηση:
Η καρίνα του σκάφους δέχεται από το νερό δύναμη κάθετη προς την κατεύθυνση πλεύσης και δύναμη αντίθετη προς την κατεύθυνση πλεύσης. Η κατεύθυνση πλεύσης όμως καθορίζεται από τη δύναμη του αέρα στο πανί
Θεωρούμε ορθογώνιους άξονες,
Η κίνηση είναι ευθύγραμμη και κάθετα στην διεύθυνση κίνησης οι δυνάμεις ισορροπούν. Άρα:
Άρα: