Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 12585 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Γεωμετρία | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 13517 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 15-Απρ-2024 | Ύλη: | 3.1. Είδη και στοιχεία τριγώνων 3.6. Κριτήρια ισότητας ορθογώνιων τριγώνων | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Γεωμετρία | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 13517 | ||
| Ύλη: | 3.1. Είδη και στοιχεία τριγώνων 3.6. Κριτήρια ισότητας ορθογώνιων τριγώνων | ||
| Τελευταία Ενημέρωση: 15-Απρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
Δίνονται δύο οξυγώνια τρίγωνα
α)
(Μονάδες 13)
β) Τα τρίγωνα
(Μονάδες 12)
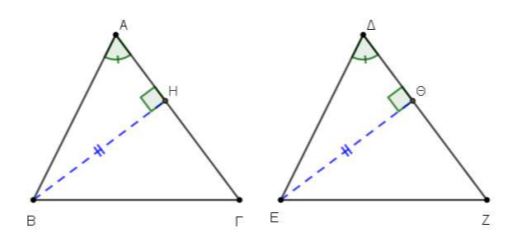

α) Συγκρίνουμε τα τρίγωνα
Επομένως, τα τρίγωνα
β) Τα τρίγωνα
Επομένως τα τρίγωνα είναι ίσα γιατί έχουν μια πλευρά και τις προσκείμενες σε αυτή γωνίες ίσες μία προς μία.
