Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 6058 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Γ' Λυκείου | |
| Κωδικός Θέματος: | 31672 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 07-Φεβ-2023 | Ύλη: | 7.3 Το φωτοηλεκτρικό φαινόμενο 7.4 Φαινόμενο Compton | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Γ' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 31672 | ||
| Ύλη: | 7.3 Το φωτοηλεκτρικό φαινόμενο 7.4 Φαινόμενο Compton | ||
| Τελευταία Ενημέρωση: 07-Φεβ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Κατά τη διάρκεια ενός πειράματος μελέτης του φωτοηλεκτρικού φαινομένου, πήραμε τη γραφική παράσταση της τάσης αποκοπής \(V_{o}\) σε συνάρτηση με τη συχνότητα της ακτινοβολίας \(f\) που προσπίπτει στην κάθοδο, όπως φαίνεται στο διάγραμμα.

4.1. Από τη μελέτη του διαγράμματος να γράψετε την εξίσωση της τάσης αποκοπής \(V_{o}\) σε συνάρτηση με τη συχνότητα της ακτινοβολίας \(f\). Ακολούθως, να αποδείξετε ότι η τιμή της σταθεράς του Planck είναι \(h=6,62\cdot 10^{-34}\ J\cdot s\).
Μονάδες 7
4.2. Να υπολογίσετε το έργο εξαγωγής του μετάλλου της επίστρωσης της επιφάνειας της καθόδου και τη συχνότητα κατωφλίου.
Μονάδες 6
Δέσμη φωτονίων μονοχρωματικής ακτινοβολίας μήκους κύματος \(λ\), προσπίπτει σε στόχο από γραφίτη και σκεδάζεται. Ανιχνεύοντας τα φωτόνια που σκεδάζονται υπό γωνία \(φ=120^{ο}\) σε σχέση με την αρχική κατεύθυνση κίνησης της δέσμης, διαπιστώνουμε ότι το μήκος κύματός τους έχει μεταβληθεί κατά \(20\%\).
Να υπολογίσετε:
4.3. το μήκος κύματος \(λ\) της προσπίπτουσας δέσμης φωτονίων.
Μονάδες 6
4.4. την κινητική ενέργεια του ανακρουόμενου ηλεκτρονίου.
Μονάδες 6
Δίνονται:
η ταχύτητα διάδοσης του φωτός \(c=3\cdot 10^{8}\ m/s\),
η μάζα του ηλεκτρονίου \(m_{e}=9\cdot 10^{-31}\ Kg\),
το ηλεκτρικό φορτίο του ηλεκτρονίου \(q_{e}=-1,6\cdot 10^{-19}\ C\),
\(συν120^{0}=-\dfrac{1}{2}\).
Τα αριθμητικά αποτελέσματα της άσκησης να υπολογιστούν με προσέγγιση δύο δεκαδικών ψηφίων.
ΘΕΜΑ 4
4.1. Η γενική μορφή της εξίσωσης της τάσης αποκοπής \(V_{o}\) σε συνάρτηση με τη συχνότητα της ακτινοβολίας \(f\) είναι:
$$V_{o}=a\cdot f+β\ \ \ \ (1)$$
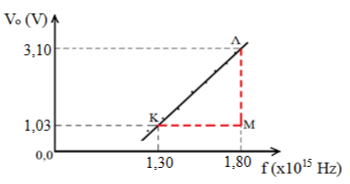
Από τις τιμές που φαίνονται στο διάγραμμα υπολογίζουμε την κλίση της ευθείας:
$$α=\dfrac{ΔV_{o}}{Δf}$$ $$=\dfrac{(ΜΛ)}{(ΚΜ)}$$ $$=\dfrac{3,10-1,03}{(1,80-1,30)\cdot 10^{15}}\cdot\ \dfrac{V}{Hz}$$ $$=4,14\cdot 10^{-15}\ V/Hz$$
Για \(f=1,30\cdot 10^{15}\ Hz\) είναι \(V_{o}=1,03\ V\), άρα από τη σχέση \((1)\) έχουμε:
$$1,03=4,14\cdot 10^{-15}\cdot 1,30\cdot 10^{15}+β $$ $$\Rightarrow β=-4,35\ V$$
Συνεπώς προκύπτει:
$$V_{o}=4,14\cdot 10^{-15}\cdot f-4,35\ \ \text{(S.I.)}\ \ \ \ (2)$$
Από τη φωτοηλεκτρική εξίσωση έχουμε:
$$Κ=hf-φ\ \ \ \ (3)$$
Εφαρμόζοντας ΘΜΚΕ για την κίνηση ενός φωτοηλεκτρονίου από την κάθοδο στην άνοδο και θέτοντας όπου \(Κ_{αν}=0\) και \(Κ_{\text{καθ}}=Κ=eV_{o}\), έχουμε:
$$|q_{e}|V_{o}=hf-φ $$ $$\Rightarrow V_{o}=\dfrac{h}{|q_{e}|}\cdot f-\dfrac{φ}{|q_{e}|}\ \ \ \ (4)$$
Συγκρίνοντας τις εξισώσεις \((2)\) και \((4)\) υπολογίζουμετην τιμή της σταθεράς του Planck:
$$\dfrac{h}{|q_{e}|}=4,14\cdot 10^{-15}\cdot \dfrac{J\cdot s}{C} $$ $$\Rightarrow h=4,14\cdot 10^{-15}\cdot 1,6\cdot 10^{-19}\ J\cdot s $$ $$\Rightarrow h=6,62\cdot 10^{-34}\ J\cdot s$$
Μονάδες 7
4.2. Συγκρίνοντας τις εξισώσεις \((2)\) και \((4)\) υπολογίζουμε το έργο εξαγωγής του μετάλλου της επίστρωσης της επιφάνειας της καθόδου:
$$ \dfrac{φ}{|q_e|}=4,35\ \dfrac{J}{C} $$ $$\Rightarrow φ=4,35\cdot 1,6\cdot 10^{-19}\ J $$ $$\Rightarrow φ=6,96\cdot 10^{-19}\ J$$
Η συχνότητα κατωφλίου \(f_{o}\) δίνεται από τη σχέση:
$$f_{o}=\dfrac{φ}{h}$$ $$=\dfrac{6,96\cdot 10^{-19}}{6,62\cdot 10^{-34}}\ Hz$$ $$=1,05\cdot 10^{15}\ Hz$$
Μονάδες 6
4.3. Αν \(λ'\) είναι το μήκος κύματος των σκεδαζόμενων φωτονίων, τότε σύμφωνα με την εξίσωση Compton έχουμε:
$$λ'-λ=\dfrac{h}{m_{e}\cdot c}(1-συνφ) $$ $$\Rightarrow λ'=λ+\dfrac{h}{m_{e}\cdot c}(1-συν120^{0}) $$ $$\Rightarrow λ'=λ+\dfrac{3}{2}\cdot \dfrac{h}{m_{e}\cdot c}\ \ \ \ (5)$$
Σύμφωνα με την εκφώνηση για την κατά \(20\%\) μεταβολή του μήκους κύματος έχουμε:
$$\dfrac{λ΄-λ}{λ}\cdot 100\%=20\% $$ $$\Rightarrow \dfrac{λ΄-λ}{λ}=0,2 $$ $$\Rightarrow λ΄=1,2λ\ \ \ \ (6)$$
Από τις σχέσεις \((5)\) και \((6)\) βρίσκουμε:
$$1,2λ=λ+\dfrac{3}{2}\cdot \dfrac{h}{m_{e}\cdot c} $$ $$\Rightarrow \dfrac{λ}{5}=\dfrac{3}{2}\cdot \dfrac{h}{m_{e}\cdot c} $$ $$\Rightarrow λ=\dfrac{15}{2}\cdot \dfrac{h}{m_{e}\cdot c} $$ $$\Rightarrow λ=1,84\cdot 10^{-11}\ m$$
Μονάδες 6
4.4. Κατά τη σκέδαση ισχύει η αρχή διατήρησης της ενέργειας. Αν \(Ε_{φ}\) είναι η ενέργεια του προσπίπτοντος φωτονίου, \(Ε_{φ}'\) είναι η ενέργεια του σκεδαζόμενου φωτονίου και \(Κ_{e}\) είναι η κινητική ενέργεια του ηλεκτρονίου μετά τη σκέδαση, τότε:
$$Ε_{φ}=Ε_{φ}'+K_{e} $$ $$\Rightarrow \dfrac{hc}{λ}=\dfrac{hc}{λ'}+K_{e} $$ $$\Rightarrow K_{e}=hc(\dfrac{1}{λ}-\dfrac{1}{λ'})\ \ \ \ (7)$$
Λαμβάνοντας υπόψη τη σχέση \((6)\), η εξίσωση \((7)\) γίνεται:
$$K_{e}=\dfrac{hc}{6λ} $$ $$\Rightarrow K_{e}=1,80\cdot 10^{-15}\ J$$
Μονάδες 6
