Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 12367 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 34323 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 23-Μαρ-2024 | Ύλη: | 2.2. Διάταξη Πραγματικών Αριθμών 3.3. Εξισώσεις 2ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 34323 | ||
| Ύλη: | 2.2. Διάταξη Πραγματικών Αριθμών 3.3. Εξισώσεις 2ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού | ||
| Τελευταία Ενημέρωση: 23-Μαρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Δίνεται το τριώνυμο:
α) Να βρείτε τη διακρίνουσα
(Μονάδες 10)
β) Για ποια τιμή του
(Μονάδες 6)
γ) Αν
i. να αποδείξετε ότι
(Μονάδες 4)
ii. να βρείτε το πρόσημο του τριωνύμου και να διατάξετε από τον μικρότερο προς τον μεγαλύτερο τους αριθμούς:
(Μονάδες 5)
ΛΥΣΗ
α) Το τριώνυμο
Επειδή
β) Το τριώνυμο έχει δύο πραγματικές ρίζες ίσες αν και μόνο αν:
γ)
i. Η σχέση
που ισχύει από υπόθεση.
iii. Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα:
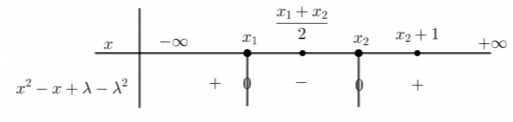
Είναι:
Άρα: