Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 6465 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Γεωμετρία | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 34488 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 18-Μαρ-2023 | Ύλη: | 4.2. Τέμνουσα δύο ευθειών - Ευκλείδειο αίτημα 4.6. Άθροισμα γωνιών τριγώνου 5.3. Ορθογώνιο 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου 5.11. Ισοσκελές τραπέζιο | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Γεωμετρία | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 34488 | ||
| Ύλη: | 4.2. Τέμνουσα δύο ευθειών - Ευκλείδειο αίτημα 4.6. Άθροισμα γωνιών τριγώνου 5.3. Ορθογώνιο 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου 5.11. Ισοσκελές τραπέζιο | ||
| Τελευταία Ενημέρωση: 18-Μαρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
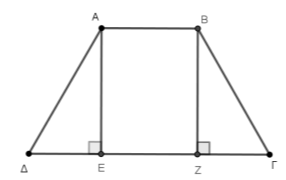
Θεωρούμε ισοσκελές τραπέζιο \(ΑΒΓΔ\) (\(ΑΒ \parallel ΓΔ\)) με \(\hat{Γ}=\hat{Δ}=60^0\). Φέρουμε τα ύψη του \(ΑΕ\) και \(ΒΖ\).
Να αποδείξετε ότι:
α) \(ΔΕ=ΓΖ\).
(Μονάδες 12)
β) Το τετράπλευρο \(ΑΕΖΒ\) είναι ορθογώνιο.
(Μονάδες 13)
ΛΥΣΗ
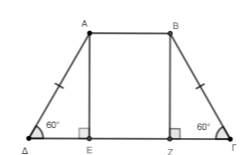
α) Αφού \(ΑΕ\) και \(ΒΖ\) είναι κάθετα στη \(ΔΓ\), τότε οι γωνίες \(\hat{ΑΕΔ}\) και \(\hat{ΒΖΓ}\) είναι ορθές και τα τρίγωνα \(ΑΕΔ\) και \(ΒΖΓ\) είναι ορθογώνια.
Για τις οξείες γωνίες του ορθογωνίου τριγώνου \(ΑΕΔ\), ισχύει \(\hat{ΔΑΕ}+\hat{Δ}=90^0\) και αφού \(\hat{Δ}=60^0\) τότε \(\hat{ΔΑΕ}=30^0\).
Οπότε, η απέναντι κάθετη πλευρά της γωνίας των \(30^0\) θα ισούται με το μισό της υποτείνουσας \(ΑΔ\), δηλαδή είναι \(ΔΕ = \dfrac{ΑΔ}{2}\).
Ομοίως, στο ορθογώνιο τρίγωνο \(ΒΖΓ\) θα είναι \(\hat{ΖΒΓ} =30^0\) και θα ισχύει \(ΖΓ = \dfrac{ΒΓ}{2}\).
Επειδή είναι \(ΑΔ =ΒΓ\) αφού το \(ΑΒΓΔ\) είναι ισοσκελές τραπέζιο από την υπόθεση, θα προκύπτει ότι \(ΔE=ΓΖ\)
β) Επειδή \(ΑΒ \parallel ΓΔ\) και το τμήμα \(ΑΕ\) είναι κάθετο στην \(ΔΓ\) από την υπόθεση, τότε θα είναι κάθετο και στην παράλληλη της \(ΔΓ\), την \(ΑΒ\).
Οπότε, το τετράπλευρο \(ΑΕΖΒ\) έχει τρείς γωνίες ορθές, τις \(\hat{ΑΕΖ}, \hat{ΒΖΕ}\) και \(\hat{EAB}\) άρα θα είναι ορθογώνιο.
