Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 7692 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 36682 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 20-Μαΐ-2023 | Ύλη: | 4.1. Ανισώσεις 1ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού 6.1. Η Έννοια της Συνάρτησης 6.2. Γραφική Παράσταση Συνάρτησης 6.3. Η Συνάρτηση ƒ(x) = αx + β | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 36682 | ||
| Ύλη: | 4.1. Ανισώσεις 1ου Βαθμού 4.2. Ανισώσεις 2ου Βαθμού 6.1. Η Έννοια της Συνάρτησης 6.2. Γραφική Παράσταση Συνάρτησης 6.3. Η Συνάρτηση ƒ(x) = αx + β | ||
| Τελευταία Ενημέρωση: 20-Μαΐ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Δίνονται η συνάρτηση
α) Να αποδείξετε ότι η γραφική παράσταση
(Μονάδες 5)
β) Να βρείτε τις τετμημένες των σημείων της
(Μονάδες 10)
γ) Έστω
(Μονάδες 10)
ΛΥΣΗ
α) Το τριώνυμο
οπότε για κάθε
Επομένως για κάθε
που σημαίνει ότι η γραφική παράσταση της
β) Οι τετμημένες των σημείων της
Το τριώνυμο
και ρίζες τις:
Το πρόσημο του τριωνύμου
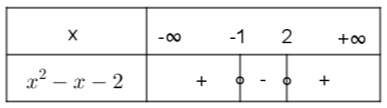
Συνεπώς:
γ) Αφού
Αφού για την τετμημένη
