Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
Έναρξη από 2 Σεπτεμβρίου
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 3167 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Γεωμετρία | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 37140 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 08-Ιουν-2023 | Ύλη: | 3.2. 1ο Κριτήριο ισότητας τριγώνων 5.2. Παραλληλόγραμμα 5.4. Ρόμβος 5.6. Εφαρμογές στα τρίγωνα 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Γεωμετρία | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 37140 | ||
| Ύλη: | 3.2. 1ο Κριτήριο ισότητας τριγώνων 5.2. Παραλληλόγραμμα 5.4. Ρόμβος 5.6. Εφαρμογές στα τρίγωνα 5.9. Μια ιδιότητα του ορθογώνιου τριγώνου | ||
| Τελευταία Ενημέρωση: 08-Ιουν-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Δίνεται ισόπλευρο τρίγωνο \(ΑΒΓ\) και τα μέσα \(Δ\), \(Ε\) και \(Μ\) των \(ΑΒ\), \(ΑΓ\) και \(ΒΓ\) αντίστοιχα. Στην προέκταση του \(ΜΔ\) (προς το \(Δ\)) θεωρούμε τμήμα \(ΔΖ=ΔΜ\).
Να αποδείξετε ότι:
α) Τα τρίγωνα \(ΑΖΔ\) και \(ΒΜΔ\) είναι ίσα.
(Μονάδες 6)
β) Το τετράπλευρο \(ΖΑΓΜ\) είναι παραλληλόγραμμο.
(Μονάδες 6)
γ) Τα τμήματα \(ΖΕ\) και \(ΑΔ\) τέμνονται κάθετα και διχοτομούνται.
(Μονάδες 7)
δ) Η \(ΒΖ\) είναι κάθετη στη \(ΖΑ\). (Μονάδες 6)
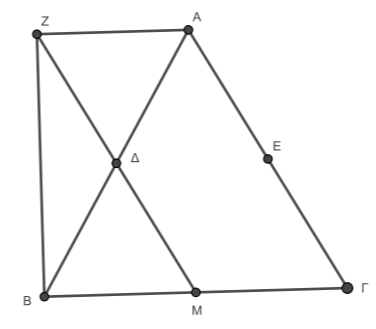
ΛΥΣΗ
α) Τα τρίγωνα \(ΑΖΔ\) και \(ΒΜΔ\) έχουν:
- \(ΔZ = ΔM\), από υπόθεση
- \(ΑΔ = ΔΒ\), διότι \(Δ\) είναι μέσο του \(ΑΒ\)
- \(\hat{AΔZ} = \hat{BΔΜ}\), ως κατακορυφήν
Τα τρίγωνα \(ΑΖΔ\) και \(ΒΜΔ\) έχουν δύο πλευρές ίσες μία προς μία και τις περιεχόμενες γωνίες ίσες άρα είναι ίσα.
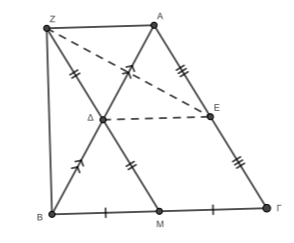
β) Το \(ΔΜ\) ενώνει τα μέσα των πλευρών \(ΑΒ\) και \(ΒΓ\) στο τρίγωνο \(ΑΒΓ\), άρα η \(ΔΜ \parallel ΑΓ\) οπότε και \(ΖΜ \parallel ΑΓ\) και \(ΔΜ = \dfrac{ΑΓ}{2}\). Όμως το \(Δ\) είναι μέσο του \(ΖΜ\) άρα \(ΔΜ = \dfrac{ΖΜ}{2}\). Συνεπώς \(ΖΜ = ΑΓ\).
Τελικά οι απέναντι πλευρές \(ΖΜ\) και \(ΑΓ\) του τετραπλεύρου \(ΖΑΓΜ\) είναι παράλληλες και ίσες οπότε το τετράπλευρο \(ΖΑΓΜ\) είναι παραλληλόγραμμο.
γ) Επειδή το \(ΖΑΓΜ\) είναι παραλληλόγραμμο ισχύει ότι \(ΖΑ \parallel ΜΓ\) δηλαδή \(ΖΑ \parallel ΒΓ\) και \(ΖΑ = ΜΓ\).
Στο τρίγωνο \(ΑΒΓ\) το \(ΔΕ\) ενώνει τα μέσα δύο πλευρών του τριγώνου οπότε:
\(ΔΕ \parallel ΒΓ\) και \(ΔΕ = \dfrac{ΒΓ}{2}\).
Όμως το \(Μ\) είναι μέσο του \(ΒΓ\) άρα \(ΔΕ = ΜΓ\).
Οπότε \(ΖΑ \parallel ΔΕ\) και \(ΖΑ = ΔΕ\), δηλαδή το τετράπλευρο \(ΖΑΕΔ\) έχει τις απέναντι πλευρές του \(ΖΑ\) και \(ΔΕ\) ίσες παράλληλες οπότε είναι παραλληλόγραμμο.
Επιπλέον ισχύει ότι: ΔΕ = \(\dfrac{ΒΓ}{2}\) και το τρίγωνο ΑΒΓ είναι ισόπλευρο οπότε \(ΒΓ = ΑΓ\). Συνεπώς \(ΔΕ = \dfrac{ΑΓ}{2}\). Όμως \(Ε\) μέσο του \(ΑΓ\) άρα \(ΑΕ = \dfrac{ΑΓ}{2}\). Οπότε \(ΔΕ = ΑΕ\).
Επομένως το παραλληλόγραμμο \(ΑΕΔΖ\) έχει τις διαδοχικές του πλευρές \(ΔΕ\) και \(ΑΕ\) ίσες οπότε είναι ρόμβος.
Τα τμήματα \(ΖΕ\), \(ΑΔ\) είναι διαγώνιοι του ρόμβου, οπότε τέμνονται κάθετα και διχοτομούνται.
δ) Είναι \(ΖΔ = ΔΜ = \dfrac{ΑΓ}{2} = \dfrac{ΑΒ}{2}\).
Στο τρίγωνο \(ΖΑΒ\) η \(ΖΔ\) είναι διάμεσος και ισούται με το μισό της πλευράς \(ΑΒ\) στην οποία αντιστοιχεί. Άρα το τρίγωνο \(ΖΑΒ\) είναι ορθογώνιο με υποτείνουσα την \(ΑΒ\), οπότε η \(ZB\) είναι κάθετη στη \(ΖΑ\).
