Λύση

α) Εφόσον το πολυώνυμο $P(x)$ έχει ακέραιους συντελεστές, οι πιθανές ακέραιες ρίζες του θα είναι οι διαιρέτες του σταθερού όρου $4$, δηλαδή οι αριθμοί $\pm 1,\pm 2,\pm 4$.

Αντικαθιστώντας στο πολυώνυμο $P(x)$ όπου $x$ τον αριθμό $2$ παρατηρούμε ότι:
$P(2)=2^3-2\cdot 2^2-2\cdot 2+4=8-8-4+4=0,$ άρα η μοναδική ακέραια ρίζα του πολυωνύμου είναι το $2$.

β) Εφόσον το $2$ είναι ρίζα του $P(x)$ ισχύει ότι το $x-2$ είναι παράγοντας του $P(x)$ οπότε εκτελώντας τη διαίρεση έχουμε:

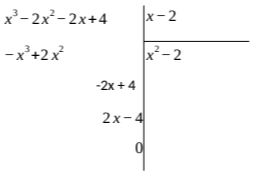
Συνεπώς, η εξίσωση γράφεται: $P(x)=0\iff (x-2)(x^2-2)=0\iff (x-2)(x-\sqrt{2})(x+\sqrt{2})=0$.
Οπότε οι ρίζες του πολυωνύμου είναι $x=2,$ $x=\sqrt{2},$ $x=-\sqrt{2}$.
Το πολυώνυμο γράφεται: $P(x)=(x-2)(x-\sqrt{2})(x+\sqrt{2})$.

Δεύτερη λύση:
Η εξίσωση $x^3-2x^2-2x+4=0$ γράφεται ισοδύναμα:

$$\begin{array}{rl}& x^3-2x^2-2x+4=0\\ & \iff x^2(x-2)-2(x-2)=0\\ & \iff (x-2)(x^2-2)=0\\ & \iff x-2=0\text{ ή }{x}^2-2=0\\ & \iff x=2\text{ ή }{x}^2=2\\ & \iff x=2\text{ ή }x=\pm \sqrt{2}.\end{array}$$

Οπότε οι ρίζες του πολυωνύμου είναι $x=2,$ $x=\sqrt{2},$ $x=-\sqrt{2}$.

Συνεπώς, η εξίσωση έχει μοναδική ακέραια ρίζα την $x=2$.

Το πολυώνυμο γράφεται: $P(x)=(x-2)(x-\sqrt{2})(x+\sqrt{2})$.