Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 10747 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 17793 | Θέμα: | 2 | |
| Τελευταία Ενημέρωση: | 16-Νοε-2024 | Ύλη: | 3.1 Τριγωνομετρικοί Αριθμοί Γωνίας | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 2 | ||
| Κωδικός Θέματος: | 17793 | ||
| Ύλη: | 3.1 Τριγωνομετρικοί Αριθμοί Γωνίας | ||
| Τελευταία Ενημέρωση: 16-Νοε-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 2
Στον τριγωνομετρικό κύκλο έχει σημειωθεί το σημείο
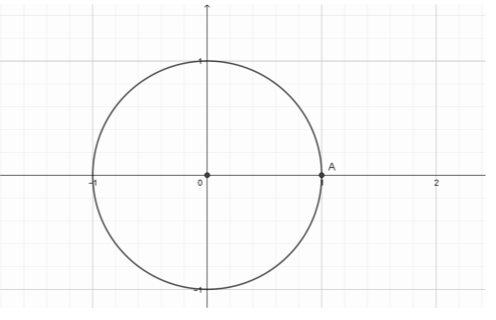
α) Να μεταφέρετε το σχήμα στην κόλα σας και να τοποθετήσετε κατά προσέγγιση στον τριγωνομετρικό κύκλο σημεία
(Μονάδες 13)
β) Για κάθε ένα τόξο του α) ερωτήματος να αποφανθείτε αν το συνημίτονο της αντίστοιχης επίκεντρης γωνίας είναι θετικός ή αρνητικός αριθμός. Να αιτιολογήσετε τις απαντήσεις σας.
(Μονάδες 12)
ΛΥΣΗ
α) Για τα τόξα
άρα το σημείο
Ακόμα:
άρα το σημείο
Τέλος:
άρα το σημείο
β) Το πρόσημο του συνημίτονου μιας γωνίας καθορίζεται από το τελικό σημείο της, ανάλογα σε ποιο τεταρτημόριο είναι. Δηλαδή θετικό, αν το τελικό σημείο είναι στο
Οπότε,