ΛΥΣΗ

α) Οι συντεταγμένες του σημείου ${\rm M}$ θα πρέπει να επαληθεύουν την εξίσωση $y=g(x)$, άρα θα ισχύει:

$$g({\displaystyle \frac{3\beta }{2}})=-3-{\displaystyle \frac{\beta }{2}}$$ $$\Rightarrow {\displaystyle \frac{3\beta }{2}}+\beta =-3-{\displaystyle \frac{\beta }{2}}$$ $$\Rightarrow {\displaystyle \frac{3\beta }{2}}+{\displaystyle \frac{\beta }{2}}+\beta =-3$$ $$\Rightarrow 3\beta =-3$$ $$\Rightarrow \beta =-1$$

β) Για $\beta =-1$:

(i) Είναι $f(x)=x^2-1$. Τα σημεία στα οποία η γραφική παράσταση της $f(x)$ τέμνει τον άξονα $x^{\prime }x$, έχουν τεταγμένη μηδέν, οπότε οι τετμημένες τους είναι λύσεις της εξίσωσης $y=f(x)=0$, άρα $x^2-1=0$ οπότε $x^2=1$. Τελικά $x=1,x=-1$.

Άρα τα σημεία στα οποία η γραφική παράσταση της $f(x)$ τέμνει τον άξονα $x^{\prime }x$ είναι τα ${\rm A}(1,0)$ και ${\rm B}(-1,0)$.

Επίσης $f(0)=0^2-1=-1$, άρα το σημείο στο οποίο η γραφική παράσταση της $f(x)$ τέμνει τον άξονα $y^{\prime }y$ είναι το $\Gamma (0,-1)$.

(ii) Θέλουμε να ισχύει $f(x)<g(x)$ δηλαδή $x^2-1<x-1$ άρα $x^2-x<0$ ή $x(x-1)<0$. Είναι φανερό ότι το πολυώνυμο $x^2-x=x(x-1)$ έχει ως ρίζες τους αριθμούς μηδέν και $1$, αφού για αυτές τις τιμές μηδενίζεται.

Δημιουργούμε τον πίνακα προσήμου, παρατηρώντας ότι ο συντελεστής του $x^2$ είναι $\alpha =1>0$.

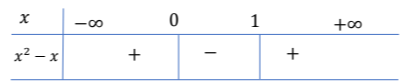
Διαπιστώνουμε ότι οι λύσεις της ανίσωσης είναι οι τιμές του $x$ μεταξύ $0$ και $1$, δηλαδή $0<x<1$.

(iii) Η εξίσωση γράφεται:

$${\displaystyle \frac{x^2-1}{x-1}}+{\displaystyle \frac{x-1}{x^2-1}}=3$$

Πρέπει $x-1\ne 0$ και $x^2-1\ne 0$.

Έτσι, για $x\ne 1$ και $x\ne -1$, η εξίσωση γράφεται:

$${\displaystyle \frac{(x-1)(x+1)}{x-1}}+{\displaystyle \frac{x-1}{(x-1)(x+1)}}=3$$

άρα:

$$x+1+{\displaystyle \frac{1}{x+1}}=3$$ $$\iff (x+1{)}^2+1=3(x+1)$$ $$\iff x^2+2x+1+1=3x+3$$ $$\iff x^2-x-1=0$$

άρα:

$$x={\displaystyle \frac{-(-1)\pm \sqrt{5}}{2}}$$ $$\Rightarrow \{\begin{array}{l}x={\displaystyle \frac{1+\sqrt{5}}{2}}\\ \\ x={\displaystyle \frac{1-\sqrt{5}}{2}}\end{array}$$