Θέμα: 35409

Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!

Τύπος Σχολείου:	Γενικό Λύκειο	Πηγή: Ι.Ε.Π.	Αναγνώσθηκε: 3651 φορές Επικοινωνία
Μάθημα:	Άλγεβρα	Τάξη:	Α' Λυκείου
Κωδικός Θέματος:	35409	Θέμα:	4
Τελευταία Ενημέρωση:	13-Νοε-2023	Ύλη:	4.2. Ανισώσεις 2ου Βαθμού 6.2. Γραφική Παράσταση Συνάρτησης
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Τύπος Σχολείου:	Γενικό Λύκειο
Τάξη:	Α' Λυκείου
Μάθημα:	Άλγεβρα
Θέμα:	4
Κωδικός Θέματος:	35409
Ύλη:	4.2. Ανισώσεις 2ου Βαθμού 6.2. Γραφική Παράσταση Συνάρτησης
Τελευταία Ενημέρωση: 13-Νοε-2023
Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida)

Αρχείο Εκφώνησης (PDF) Αρχείο Εκφώνησης (DOC)

ΘΕΜΑ 4

Δίνεται το τριώνυμο $x^{2}-λx+1$, με παράμετρο $λ\in \mathbb{R}$.

α) Να αποδείξετε ότι η διακρίνουσα του τριωνύμου είναι $Δ=λ^{2}-4$.
(Μονάδες 05)

β) Θεωρούμε τις συναρτήσεις $f$, $g$ που είναι ορισμένες στο $\mathbb{R}$ με: $f(x)=λx-λ+2$ και $g(x)=x^{2}-λ+3$, $λ\in \mathbb{R}$.

Να αποδείξετε ότι η εξίσωση από την οποία μπορούμε να βρούμε τις τετμημένες των κοινών σημείων των γραφικών παραστάσεων των $f$ και $g$ είναι ισοδύναμη με την εξίσωση $x^{2}-λx+1=0$.
(Μονάδες 05)
Στο καθένα από τα επόμενα σχήματα δίνεται οι γραφικές παραστάσεις των δυο συναρτήσεων για διαφορετικές τιμές της παραμέτρου $λ$.
Με δεδομένο ότι $λ\in {1,2,4}$, να βρείτε την τιμή της παραμέτρου $λ$ σε καθένα από τα σχήματα, δικαιολογώντας την απάντηση σας.
(Μονάδες 15)

Εμφάνιση Απάντησης

Αρχείο Απάντησης (PDF) Αρχείο Απάντησης (DOC)

ΛΥΣΗ

α) Το τριώνυμο $x^{2}-λx+1$ έχει: $α=1$, $β=-λ$, $γ=1$.

Έχουμε:

$$Δ=β^{2}-4αγ$$ $$=(-λ)^{2}-4\cdot 1\cdot 1$$ $$=λ^{2}-4,\ λ\in \mathbb{R}$$

β)

Για να βρούμε τις τετμημένες των κοινών σημείων των $C_{f}$, $C_{g}$ πρέπει και αρκεί να λύσουμε την εξίσωση $g(x)=f(x)$.

Έχουμε διαδοχικά:

$$g(x)=f(x) $$ $$\Leftrightarrow x^{2}-λ+3=λx-λ+2 $$ $$\Leftrightarrow x^{2}-λx+1=0$$
Για $λ=1$ έχουμε: $Δ=1^{2}-4=-3 < 0$.
Για $λ=2$ έχουμε: $Δ=2^{2}-4=0$.
Για $λ=4$ έχουμε: $Δ=4^{2}-4=12 > 0$.

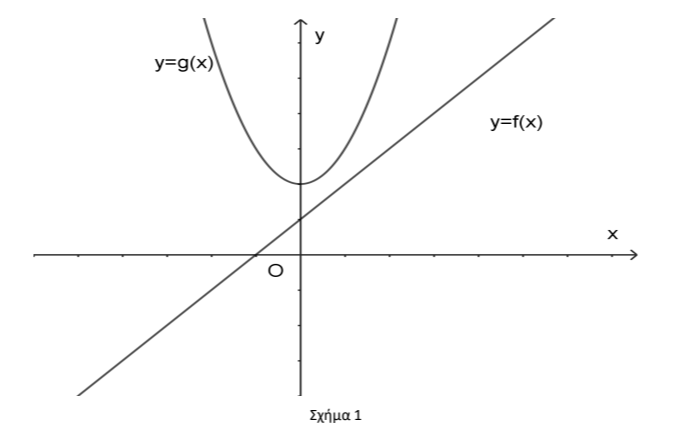
Για το σχήμα 1: Παρατηρούμε ότι η γραφική παράσταση της συνάρτησης $g$ βρίσκεται πάνω από την γραφική παράσταση της συνάρτησης για κάθε $x\in \mathbb{R}$, επομένως ισχύει:

$$g(x)>f(x)\ \ \ \ (1)$$

για κάθε $x\in \mathbb{R}$.

Έχουμε:

$$(1) \Leftrightarrow x^{2}-λ+3>λx-λ+2 $$ $$\Leftrightarrow x^{2}-λx+1>0$$

για κάθε $x\in \mathbb{R}$.

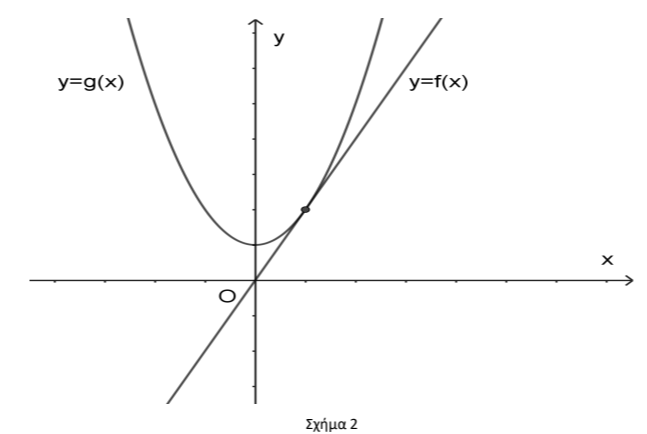
Γνωρίζουμε ότι το τριώνυμο $x^{2}-λx+1$ έχει σταθερό πρόσημο όταν $Δ < 0$ επομένως η τιμή του $λ$ που αντιστοιχεί στο σχήμα αυτό είναι $λ=1$.

Για το σχήμα 2: Παρατηρούμε ότι οι γραφικές παραστάσεις των δύο συναρτήσεων έχουν ακριβώς ένα κοινό σημείο, επομένως η εξίσωση $g(x)=f(x)\ \ (2)$ έχει μία διπλή ρίζα.
Έχουμε:

$$(2) \Leftrightarrow x^{2}-λ+3=λx-λ+2 $$ $$\Leftrightarrow x^{2}-λx+1=0$$

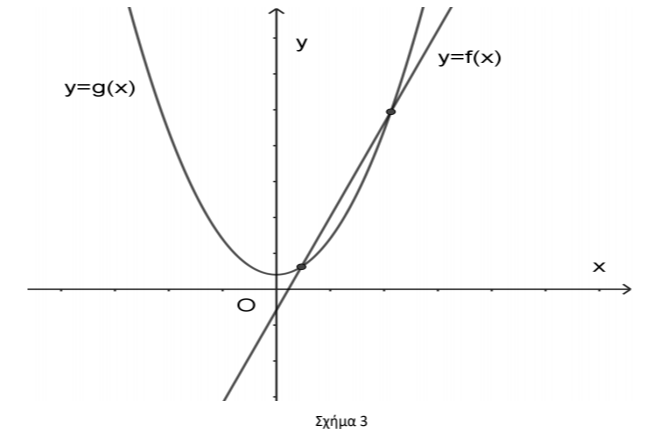
Γνωρίζουμε ότι το τριώνυμο $x^{2}-λx+1$ έχει μία διπλή ρίζα όταν $Δ=0$ επομένως η τιμή του $λ$ που αντιστοιχεί στο σχήμα αυτό είναι $λ=2$.

Για το σχήμα 3: Παρατηρούμε ότι οι γραφικές παραστάσεις των δύο συναρτήσεων έχουν δύο κοινά σημεία, επομένως η εξίσωση $g(x)=f(x)\ \ (3)$ έχει δύο άνισες λύσεις.

Όπως και στην δεύτερη περίπτωση η εξίσωση $(3)$ είναι ισοδύναμη με την εξίσωση $x^{2}-λx+1=0$.

Γνωρίζουμε ότι το τριώνυμο $x^{2}-λx+1$ έχει δύο άνισες λύσεις όταν $Δ>0$ επομένως η τιμή του $λ$ που αντιστοιχεί στο σχήμα αυτό είναι $λ=4$.