Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 3441 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 11647 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 15-Απρ-2024 | Ύλη: | ||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 11647 | ||
| Ύλη: | |||
| Τελευταία Ενημέρωση: 15-Απρ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ Δ
Ένας κύβος μάζας \(10 kg\) ολισθαίνει πάνω σε λείο δάπεδο με σταθερή ταχύτητα, μέτρου \(υ_{0} = 3 m/s\), κατά μήκος μιας ευθείας που ταυτίζεται με τον οριζόντιο άξονα \(x'x\). Τη χρονική στιγμή \(t= 0 s\) όπου ο κύβος διέρχεται από τη θέση \(x = 0 m\) του άξονα κινούμενος προς τη θετική φορά αρχίζει να ασκείται σε αυτόν οριζόντια δύναμη \(\vec{F}\) ίδιας κατεύθυνσης με την ταχύτητα. Το μέτρο της δύναμης μεταβάλλεται με την θέση \(x\) του κύβου, σύμφωνα με την σχέση \(F = 10 \cdot x\) όπου (\(F\) σε \(Ν\) και \(x\) σε \(m\)). Τη χρονική στιγμή που ο κύβος διέρχεται από τη θέση \(x= 4\ m\) η δύναμη \(\vec{F}\) παύει να ασκείται. Αμέσως μετά την κατάργηση της \(\vec{F}\) ο κύβος εισέρχεται σε τραχύ οριζόντιο δάπεδο, μέχρι να σταματήσει να κινείται. Η κίνηση στο τραχύ δάπεδο διαρκεί χρόνο ίσο με \(2,5 s\). Δίνεται η επιτάχυνση της βαρύτητας, \(g = 10\frac{m}{s^{2}}\).
Δ1) Να υπολογίσετε το μέτρο της επιτάχυνσης του κύβου στη θέση \(x = 2\ m\).
Μονάδες 5
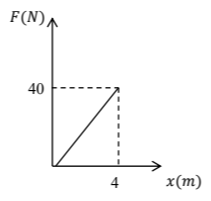
Δ2) Να κατασκευάσετε το διάγραμμα του μέτρου της δύναμης \(\vec{F}\) σε συνάρτηση με τη θέση \(x\) για τη μετατόπιση από \(0 \rightarrow 4\ m\). Στη συνέχεια να υπολογίσετε την ενέργεια που μεταφέρθηκε στον κύβο, μέσω του έργου της δύναμης \(\vec{F}\), κατά τη διάρκεια της μετατόπισης του κύβου από τη θέση \(x= 0\ m\) έως τη θέση \(x = 4\ m\).
Μονάδες 7
Δ3) Να υπολογίσετε το μέτρο της ταχύτητας του κύβου στη θέση \(x= 4\ m\).
Μονάδες 6
Δ4) Να υπολογίσετε το συντελεστή τριβής ολίσθησης μεταξύ κύβου-δαπέδου στο τραχύ δάπεδο.
Μονάδες 7
Ενδεικτική λύση
Δ1) Στη θέση \(x= 2\ m\) η δύναμη έχει μέτρο \(F=10\cdot 2=20\ N\) και θετική φορά. Εφαρμόζοντας το 2ο νόμο του Newton υπολογίζεται η επιτάχυνση του κύβου στο λείο δάπεδο:
Δ2) Το εμβαδό που περικλείεται από τη γραφική παράσταση δύναμης θέσης \((F=f(x))\) και του άξονα των θέσεων, είναι αριθμητικά ίσο με το έργο της δύναμης \(\vec{F}\) μέσω του οποίου προσφέρεται ενέργεια στο κιβώτιο:
$$W_{F}=\dfrac{40\cdot 4}{2}$$ $$W_{F}=80\ J$$
Δ3) Εφαρμόζουμε το Θεώρημα Μεταβολής της Κινητικής Ενέργειας – Έργου (ΘΜΚΕ) από τη θέση \(x= 0\) έως τη θέση \(x = 4\ m\):
$$Κ_{\text{τελ}}-Κ_{\text{αρχ}}=W_{F}$$ $$\dfrac{1}{2}mυ^{2}-\dfrac{1}{2}mυ_{0}^{2}=W_{F}$$ $$υ=5 \frac{m}{s}$$
Δ4) Αρχικά υπολογίζουμε την επιβράδυνση στο τραχύ δάπεδο όπου στον κύβο ασκούνται οι δυνάμεις που απεικονίζονται στο σχήμα:
$$α=\dfrac{Δυ}{Δt}$$ $$α=\dfrac{0-5}{2,5} \dfrac{m}{s^{2}}$$ $$α=-2\dfrac{m}{s^{2}}$$
Στη συνέχεια εφαρμόζουμε τον 1ο νόμο του Newton στον κατακόρυφο άξονα:
$$ΣF_{ψ}=0$$ $$Ν=m\cdot g$$ $$Ν=100Ν$$
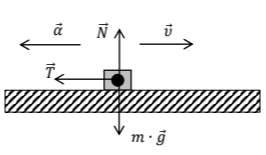
Και τον 2ο νόμο του Newton στον οριζόντιο άξονα λαμβάνοντας ως θετική τη φορά της επιβράδυνσης:
$$Τ=m\cdot a$$ $$Τ=20Ν$$
Άρα \(Τ=μ\cdot Ν \Rightarrow μ=0,2\)