Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 8624 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 14744 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 06-Οκτ-2023 | Ύλη: | 2.1. Οι Πράξεις και οι Ιδιότητές τους 2.2. Διάταξη Πραγματικών Αριθμών 6.2. Γραφική Παράσταση Συνάρτησης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 14744 | ||
| Ύλη: | 2.1. Οι Πράξεις και οι Ιδιότητές τους 2.2. Διάταξη Πραγματικών Αριθμών 6.2. Γραφική Παράσταση Συνάρτησης | ||
| Τελευταία Ενημέρωση: 06-Οκτ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
α) Να αποδείξετε ότι \(x -x^{2}\le \dfrac{1}{4}\) για κάθε πραγματικό αριθμό \(x\). Πότε ισχύει το ίσον;
(Μονάδες 8)
β) Στο παρακάτω σχήμα έχει σχεδιασθεί η γραφική παράσταση \((ε)\) της συνάρτησης \(f(x)=1 – x\), \(x\in \mathbb{R}\), η οποία τέμνει τους άξονες \(x'x\) και \(y'y\) στα σημεία \(Ε\) και \(Δ\) αντίστοιχα. Ένα μεταβλητό σημείο \(Α\), με τετμημένη \(α\), κινείται επί της ευθείας \((ε)\) και μεταξύ των σημείων \(Δ\) και \(Ε\). Φέρνουμε από το \(Α\) καθέτους στους άξονες και έστω \(Β\) και \(Γ\) τα σημεία τομής με \(y'y\) και \(x'x\) αντίστοιχα.
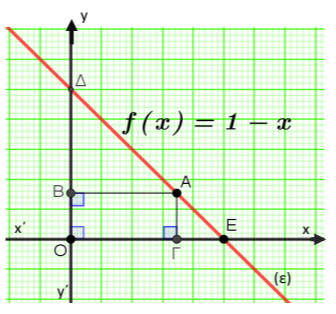
Να βρείτε το εμβαδόν του ορθογωνίου \(ΑΒΟΓ\).
(Μονάδες 10)Να αποδείξετε ότι η μεγαλύτερη δυνατή τιμή του εμβαδού του μεταβλητού ορθογωνίου \(ΑΒΟΓ\) είναι \(\dfrac{1}{4}\). Για ποια θέση του σημείου \(Α\) επιτυγχάνεται αυτή η τιμή;
(Μονάδες 7)
ΛΥΣΗ
α)
$$x -x^{2}\le \dfrac{1}{4} $$ $$\Leftrightarrow x^{2}- x+\dfrac{1}{4}\ge 0 $$ $$\Leftrightarrow x^{2}- 2\cdot x\cdot \dfrac{1}{2}+(\dfrac{1}{2})^{2}\ge 0 $$ $$\Leftrightarrow (x-\dfrac{1}{2})^{2}\ge 0,\ \ \text{ισχύει}$$
Το ίσον ισχύει αν και μόνον αν:
$$x -\dfrac{1}{2}=0 $$ $$\Leftrightarrow x=\dfrac{1}{2}$$
β)
Αρχικά παρατηρούμε ότι το σημείο \(Δ\) έχει τετμημένη μηδέν και τεταγμένη \(f(0)=1,\) ενώ αν είναι \(k\) η τετμημένη του σημείου \(Ε\), η τεταγμένη του θα είναι \(f(k) =0 = 1 - k\), άρα \(k=1\). Ώστε \(Δ(0,1)\) και \(Ε(1,0)\).
Έστω τώρα ότι \(α\) είναι η τετμημένη του σημείου \(Α\), με \(0\le α\le 1\), οπότε το σημείο \(Α\) έχει τεταγμένη \(f(α)=1 – α\).
Έτσι έχουμε \(Γ(α, 0)\), \(Α(α, 1 - α)\), \(Β(0, 1- α)\).
Επομένως το εμβαδόν του ορθογωνίου \(ΑΒΟΓ\) είναι \(Ε = α\cdot (1 - α)=α -α^{2}\).
Σύμφωνα με το α) ερώτημα είναι \(Ε\le \dfrac{1}{4}\), δηλαδή για οποιαδήποτε τιμή του \(α\), το εμβαδόν του ορθογωνίου γίνεται το πολύ \(\dfrac{1}{4}\). Το ίσον ισχύει αν και μόνον αν \(α=\dfrac{1}{2}\), οπότε σε αυτή την περίπτωση είναι \(Α(\dfrac{1}{2},\dfrac{1}{2})\), δηλαδή το \(ΑΒΟΓ\) θα γίνει τετράγωνο.
