Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 64005 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική Προσανατολισμού | Τάξη: | Β' Λυκείου | |
| Κωδικός Θέματος: | 16136 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 08-Μαΐ-2022 | Ύλη: | 1.1 Οριζόντια βολή | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Β' Λυκείου | ||
| Μάθημα: | Φυσική Προσανατολισμού | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 16136 | ||
| Ύλη: | 1.1 Οριζόντια βολή | ||
| Τελευταία Ενημέρωση: 08-Μαΐ-2022 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
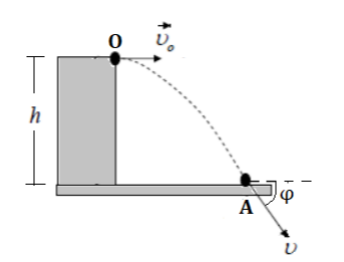
Σφαίρα μάζας \(𝑚=0,1Kg\) βάλλεται οριζόντια με ταχύτητα μέτρου \(υ_ο=20 \ m/s\) από την ταράτσα ενός κτιρίου ύψους \(h\) από το έδαφος. Όταν πέφτει στο έδαφος η σφαίρα η ταχύτητά της σχηματίζει με αυτό γωνία \(φ=45^0\) (όπως φαίνεται στο παραπάνω σχήμα).
4.1. Να υπολογίσετε την κινητική ενέργεια της σφαίρας όταν φτάνει στο έδαφος.
Μονάδες 6
4.2. Να βρεθεί το ύψος \(h\) του κτιρίου.
Μονάδες 6
4.3. Να υπολογίσετε τη δυναμική ενέργεια της σφαίρας τη χρονική στιγμή \(𝑡_1=1 \ 𝑠\).
Ως επίπεδο μηδενικής δυναμικής ενέργειας να θεωρήσετε το έδαφος.
Μονάδες 6
4.4. Να υπολογίσετε την κινητική ενέργεια της σφαίρας τη χρονική στιγμή \(t_2\), όπου η οριζόντια μετατόπιση της σφαίρας είναι οκταπλάσια της κατακόρυφης μετατόπισής της.
Μονάδες 7
Δίνεται η επιτάχυνση βαρύτητας \(g_o=10 \ m/s^2\).
ΘΕΜΑ 4
4.1. Η σφαίρα εκτελεί οριζόντια βολή. Συνεπώς στον οριζόντιο άξονα \(Οx\) εκτελεί ευθύγραμμη ομαλή κίνηση, οπότε:
$$𝜐_𝑥=υ_0, \ (1)$$ $$\text{ και } 𝑥=υ_0 t, \ (2)$$
Στον κατακόρυφο άξονα \(Οy\) εκτελεί ελεύθερη πτώση, οπότε:
$$υ_y=gt, \ (3)$$ $$\text{ και } y=\dfrac{1}{2}gt^2,\ (4)$$
Όταν φτάσει στο έδαφος, από τη σχέση (1) έχουμε:
$$υ_x=υ_0$$ $$⇒υσυνφ=υ_0$$ $$⇒υ=\dfrac{υ_0}{συνφ}$$ $$⇒υ=20\sqrt{2} \ m/s$$
Άρα:
\(Κ=\dfrac{1}{2}mυ^2= \ 40 J\)
Μονάδες 6
4.2. Από τη σχέση (3) έχουμε:
$$υ_y=gt$$ $$⇒υημφ=gt$$ $$⇒t=\dfrac{υημφ}{g}$$ $$⇒t= 2 \ s$$ οπότε σύμφωνα με τη σχέση (4) έχουμε:
$$h=\dfrac{1}{2}g𝑡^2$$ $$⇒h=20 \ m$$
Μονάδες 64.3. Από τη σχέση (4) έχουμε:
$$y_1=\dfrac{1}{2}gt^2_1$$ $$⇒y_1=5 \ m$$
Άρα η δυναμική ενέργεια της σφαίρας είναι:$$U=mg(h− y_1)=15 \ J$$
Μονάδες 6
4.4. Από τις σχέσεις \((2)\) και \((4)\) έχουμε:
$$x=8y\Rightarrow υ_0t_2 =8\cdot \dfrac{1}{2}gt^2_2$$ $$⇒t_2 =0,5 \ s$$
Άρα η ταχύτητα της σφαίρας είναι:
$$υ_2=\sqrt{υ^2_{2𝑥}+υ^2_{2𝑦}}=\sqrt{υ^2_0+(gt_2)^2}=\sqrt{425} \ m/s$$ $$\text{οπότε: }Κ_2=\dfrac{1}{2}mυ^2_2=21,25 \ J$$
Μονάδες 7