Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 7327 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Άλγεβρα | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 14645 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 21-Μαρ-2023 | Ύλη: | 5.3. Γεωμετρική πρόοδος | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Άλγεβρα | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 14645 | ||
| Ύλη: | 5.3. Γεωμετρική πρόοδος | ||
| Τελευταία Ενημέρωση: 21-Μαρ-2023 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ 4
Ένας ζωγράφος ξεκινώντας από ένα τετράγωνο πλευράς
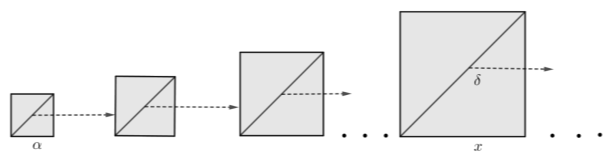
α) i. Αν η πλευρά ενός τετραγώνου έχει μήκος
(Μονάδες 4)
ii. Να αποδείξετε ότι τα εμβαδά των διαδοχικών τετραγώνων είναι όροι γεωμετρικής προόδου
(Μονάδες 7)
β) Αν το εμβαδόν του τέταρτου κατά σειρά τετραγώνου ισούται με
i. την πλευρά
(Μονάδες 8)
ii. το πλήθος των αρχικών τετραγώνων με συνολικό εμβαδόν
(Μονάδες 6)
α) i. Από το πυθαγόρειο θεώρημα προκύπτει ότι για τη διαγώνιο
και επειδή
ii. Από το ερώτημα (α.i) προκύπτει ότι αν ένα από τα τετράγωνα της ακολουθίας έχει πλευρά
και είναι σταθερός. Οπότε, τα εμβαδά των τετραγώνων είναι διαδοχικοί όροι γεωμετρικής προόδου με λόγο
Ο γενικός όρος της προόδου δίνεται από τη σχέση
β)
- Ισχύει ότι
- Το άθροισμα των
Για να είναι το συνολικό εμβαδών των αρχικών τετραγώνων ίσο με
Άρα, το πλήθος των τετραγώνων που έχουν συνολικό εμβαδόν