Για να εκτυπώσετε το Θέμα πατήστε "Εκτύπωση"!
| Τύπος Σχολείου: | Γενικό Λύκειο | Πηγή: Ι.Ε.Π. | Αναγνώσθηκε: 6670 φορές Επικοινωνία | |
|---|---|---|---|---|
| Μάθημα: | Φυσική | Τάξη: | Α' Λυκείου | |
| Κωδικός Θέματος: | 11667 | Θέμα: | 4 | |
| Τελευταία Ενημέρωση: | 24-Οκτ-2024 | Ύλη: | Χωρίς Αντιστοίχιση Ύλης | |
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | ||||
| Τύπος Σχολείου: | Γενικό Λύκειο | ||
|---|---|---|---|
| Τάξη: | Α' Λυκείου | ||
| Μάθημα: | Φυσική | ||
| Θέμα: | 4 | ||
| Κωδικός Θέματος: | 11667 | ||
| Ύλη: | Χωρίς Αντιστοίχιση Ύλης | ||
| Τελευταία Ενημέρωση: 24-Οκτ-2024 | |||
| Το θέμα προέρχεται και αντλήθηκε από την πλατφόρμα της Τράπεζας Θεμάτων Διαβαθμισμένης Δυσκολίας που αναπτύχθηκε (MIS5070818-Tράπεζα θεμάτων Διαβαθμισμένης Δυσκολίας για τη Δευτεροβάθμια Εκπαίδευση, Γενικό Λύκειο-ΕΠΑΛ) και είναι διαδικτυακά στο δικτυακό τόπο του Ινστιτούτου Εκπαιδευτικής Πολιτικής (Ι.Ε.Π.) στη διεύθυνση (http://iep.edu.gr/el/trapeza-thematon-arxiki-selida) | |||
ΘΕΜΑ Δ
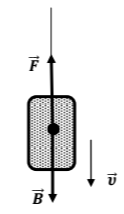
O θάλαμος ανελκυστήρα μάζας
Στο θάλαμο εκτός από το βάρος του ασκείται, μέσω ενός συρματόσχοινου, μία κατακόρυφη προς τα πάνω δύναμη
Η τιμή της
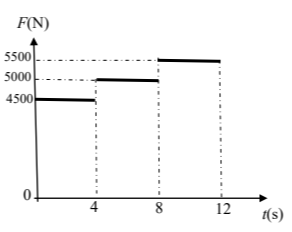
Δίνεται η επιτάχυνση της βαρύτητας ίση με
Δ1) Να χαρακτηρίσετε τις κινήσεις που εκτελεί ο θάλαμος και να υπολογίσετε την τιμή της επιτάχυνσής του σε κάθε μία από αυτές.
Μονάδες 6
Δ2) Να υπολογίσετε το μέτρο της ταχύτητας του θαλάμου τις χρονικές στιγμές
Μονάδες 6
Δ3) Να σχεδιάσετε το διάγραμμα της ταχύτητας του θαλάμου συναρτήσει του χρόνου και να υπολογίσετε το ολικό μήκος της διαδρομής που έκανε ο ανελκυστήρας κατά την κάθοδό του.
Μονάδες 8
Δ4) Να υπολογίστε το έργο της δύναμης
Μονάδες 5
Ενδεικτική Λύση
Δ1) Το βάρος του θαλάμου είναι:
- Χρονικό διάστημα
Ευθύγραμμη ομαλά επιταχυνόμενη κίνηση με μηδενική αρχική ταχύτητα.
- Χρονικό διάστημα
Ευθύγραμμη ομαλή κίνηση.
- Χρονικό διάστημα
Ευθύγραμμη ομαλά επιβραδυνόμενη κίνηση.
Από το 2ο νόμο του Nεύτωνα έχουμε:
- Χρονικό διάστημα
- Χρονικό διάστημα
- Χρονικό διάστημα
Δ2) Για τις ταχύτητες έχουμε:
- Χρονική στιγμή
- Χρονική στιγμή
- Χρονική στιγμή
Δ3)
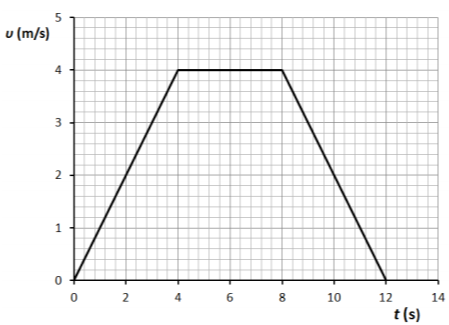
Το ολικό μήκος της διαδρομής είναι ίσο με το εμβαδό του τραπεζίου:
Δ4)
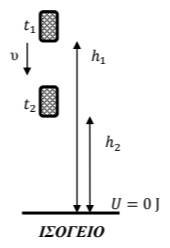
Η μετατόπιση του θαλάμου από τη χρονική στιγμή
και τo έργο της δύναμης
Η μεταβολή της δυναμικής ενέργειας του θαλάμου στο ίδιο χρονικό διάστημα είναι:
